Upper and lower bounds on the beta function
The beta function B(x, y) is defined by
and is the normalizing constant for the beta probability distribution. It is related to the gamma function via
The beta function comes up often in applications. It can be challenging to work with, however, and so estimates for the function are welcome.
The function 1/xy gives simple approximation and upper bound for B(x, y). Alzer [1] proved that when x > 1 and y > 1
where the constant b is defined by
Cerone [2] gives a different bound which varies with x and y and is usually better than Alzer's bound. For x and y greater than 1, Cerone shows
where
and
Cerone's bound is slightly larger in the worst case, near x = y = (3 + 5)/2, but is smaller in general.
The difference between B(x, y) and 1/xy is largest when x or y is small. We can visualize this with the Mathematica command
Plot3D[Beta[x, y] - 1/(x y), {x, 0.5, 2.5}, {y, 0.5, 2.5}]which produces the following plot.
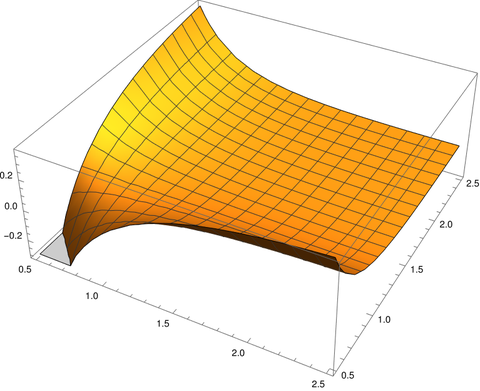
The plot dips down in the corner where x and y are near 0.5 and curls upward on the edges where one of the variables is near 0.5 and the other is not.
Let's look at B(x, y) and 1/xy at along a diagonal slice (3t, 4t).
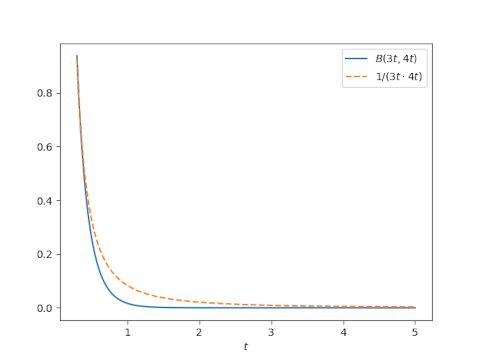
This suggests that approximating B(x, y) with 1/xy works best when the arguments are either small or large, with the maximum difference being when the arguments are moderate-sized. In the plot we see B(3, 4) is not particularly close to 1/12.
Next lets look at 1/xy - B(x, y) along the same diagonal slice.
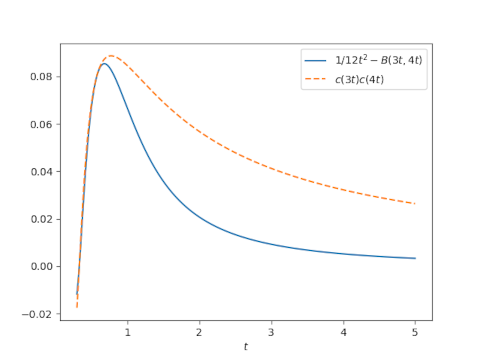
This shows that the error bound C(x) C(y) is not too tight, but better than the constant bound except near the maximum of 1/xy - B(x, y).
Related posts- Gauss' constant
- Beta inequalities with integer parameters
- Predictive probability for large populations
[1] H. Alzer. Monotonicity properties of the Hurwitz zeta function. Canadian Mathematical Bulletin 48 (2005), 333-339.
[2] P. Cerone. Special functions: approximations and bounds. Applicable Analysis and Discrete Mathematics, 2007, Vol. 1, No. 1, pp. 72-91
The post Upper and lower bounds on the beta function first appeared on John D. Cook.