Finding the imaginary part of an analytic function from the real part
A function f of a complex variable z = x +iy can be factored into real and imaginary parts:
where x and y are real numbers, and u and v are real-valued functions of two real values.
Suppose you are given u(x, y) and you want to find v(x, y). The function v is called a harmonic conjugate of u.
Finding vIf u and v are the real and imaginary parts of an analytic function, then u and v are related via the Cauchy-Riemann equations. These are first order differential equations that one could solve to find u given v or v given u. The approach I'll present here comes from [1] and relies on algebra rather than differential equations.
The main result from [1] is
So given an expression for u (or v) we evaluate this expression at z/2 and z/2i to get an expression for f, and from there we can find an expression for v (or u).
This method is simpler in practice than in theory. In practice we're just plugging (complex) numbers into equations. In theory we'd need to be a little more careful in describing what we're doing, because u and v are not functions of a complex variable. Strictly speaking the right hand side above applies to the extensions of u and v to the complex plane.
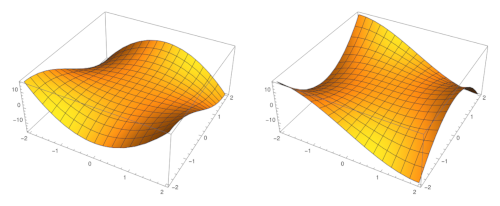
Shaw gives three exercises for the reader in [1]. The first is
We find that
We know that the constant term is purely imaginary because u(0, 0) = 0.
Then
and so
is a harmonic conjugate for u for any real number .
The image above is a plot of the function u on the left and its harmonic conjugate v on the right.
Example 2Shaw's second example is
We begin with
and so
From there we find
Shaw's last exercise is
Then
This leads to
from which we read off
[1] William T. Shaw. Recovering Holomorphic Functions from Their Real or Imaginary Parts without the Cauchy-Riemann Equations. SIAM Review, Dec., 2004, Vol. 46, No. 4, pp. 717-728.
The post Finding the imaginary part of an analytic function from the real part first appeared on John D. Cook.