Solitons and the KdV equation
Rarely does a nonlinear differential equation, especially a nonlinear partial differential equation, have a closed-form solution. But that is the case for the Korteweg-De Vries equation.
(Technically I should say it's rare for a naturally-occurring nonlinear differential equation to have a closed-form solution. You can always start with a solution and cook up a contrived differential equation that it satisfies, but that differential equation will not be one that is interesting in applications.)
The Korteweg-De Vries (KdV) equation is
This equation is used to model shallow water waves.
The KdV equation is a third-order PDE, which is unusual but not unheard of. As I wrote about earlier in the context of ODEs, third order linear equations are virtually nonexistent in application, but third order nonlinear equations are not so uncommon.
The function
is a solution to the KdV equation. It is an example of a class of functions known as solitons.
You can increase the amplitude by increasing v, but when you do you also increase the velocity of the wave. You can't vary amplitude and velocity independently because the KdV equation is nonlinear.
Verifying by hand that this is a solution is tedious, so I'll show the verification in Mathematica.
u[x_, t_] := - (v/2) Sech[Sqrt[v] (x - v t - a)/2]^2 Simplify[ D[u2[x, t], {t, 1}] - 6 u2[x, t] D[u2[x, t], {x, 1}] + D[u2[x, t], {x, 3}] ]This returns 0. (Without the Simplify[] command it returns a mess, but the mess simplifies to 0.)
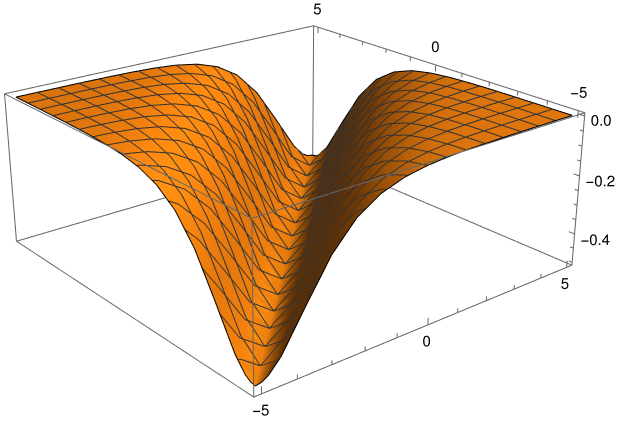
Here's a plot of the soliton with a = 0 and v = 1.
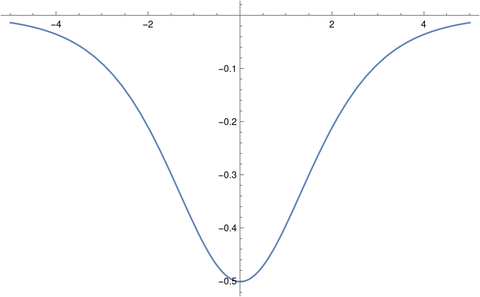
Here's a slice with x = 0.
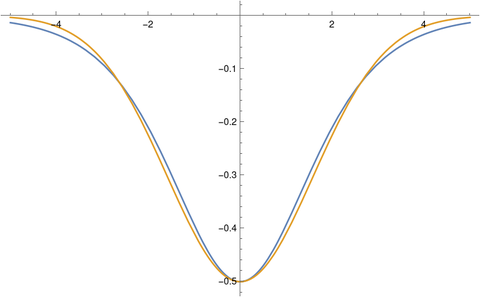
This looks remarkably like the density function of a Gaussian turned upside down. Here's a plot with the soliton (in blue) with the density of a normal random variable with variance 5/2, scaled to have the same amplitude at 0.
- Types of nonlinearity in PDEs
- Trading generalized derivatives for classical derivatives
- Partial differential equations consulting