Rational solution to Korteweg–De Vries equation

Students seeing differential equations for the first time expect every equation to have a nice closed-form solution, because up to that point in their education nearly every problem they've seen has been contrived to have a nice closed-form solution.

Once you resign yourself to the fact that a differential equation will rarely have a closed form solution, it's a treat when you run across one that does. This is especially true for nonlinear equations.

The Korteweg-De Vries (KdV) equation is

is such a treat. I wrote a few days ago about the sech^2 solution to the KdV equation.

There's also a rational solution:

We can verify this is a solution to the KdV equation reusing the Mathematica code from the earlier post.

 u[x_, t_] := u[x_, t_] := 6 x (x^3 - 24 t)/(x^3 + 12 t)^2 Simplify[ D[u[x, t], {t, 1}] - 6 u[x, t] D[u[x, t], {x, 1}] + D[u[x, t], {x, 3}] ]

This simplifies to 0.

Here's a plot:

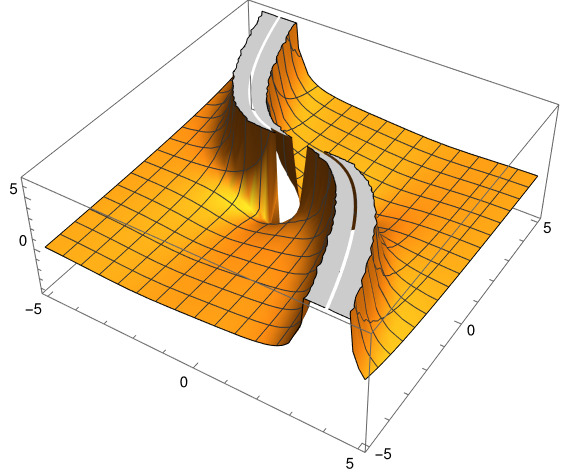
The top of the plot looks like a two-lane road on top of a mountain ridge, with a sinkhole in the middle of the road.

The road" is a artifact of plotting. The solution is singular along the curve x^3 + 12t= 0, and Mathematica had to chop the top of the graph off because it can't plot an infinitely tall function.

The post Rational solution to Korteweg-De Vries equation first appeared on John D. Cook.