A very accurate logarithm approximation

The previous post looked at an efficient way to approximate nth roots of fractions near 1 by hand. This post does the same for logarithms.

As before, we assume x = p/q and define

s = p + q
d = p - q

Because we're interested in values of x near 1, d is small, and small numbers are convenient to work with by hand.

In [1] Kellogg gives the approximation

log x 3(x^2 - 1)/((x+ 1)^2 + 2x) = 6ds/(3s^2 - d^2)

So, for example, suppose we wanted to take the natural log of 7/8. then p = 7, q = 8, s = 15, and d = -1.

log x (6*15*(-1))/(3*225 - 1) = - 90/674 = - 45/337.

This approximation is good to six decimal places.

Kellogg claims that

This value of E [the natural logarithm], if q [what I've called x] be between .9 and 1.1, is true to the seventh decimal.

He then goes on to explain how to create an even more accurate approximation, and how to deal with larger values of x.

Here's a plot verifying Kellogg's claim.

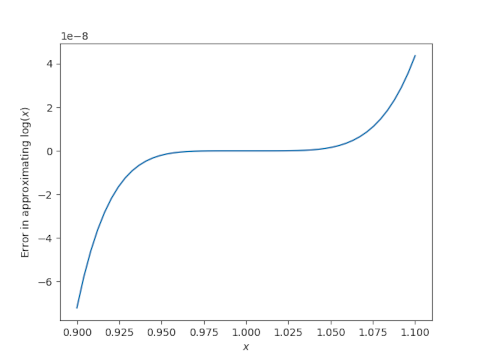
Note the that scale of the plot is 10^-8. As the flat spot in the middle suggests, you get even more decimal places for x closer to 1.

[1] Ansel N. Kellogg. Empirical formulae; for Approximate Computation. The American Mathematical Monthly. February 1987, Vol. 4 No. 2, pp. 39-49.

The post A very accurate logarithm approximation first appeared on John D. Cook.