Fitting a line without an intercept term

The other day I was looking at how many lumens LED lights put out per watt. I found some data on Wikipedia, and as you might expect the relation between watts and lumens is basically linear, though not quite.

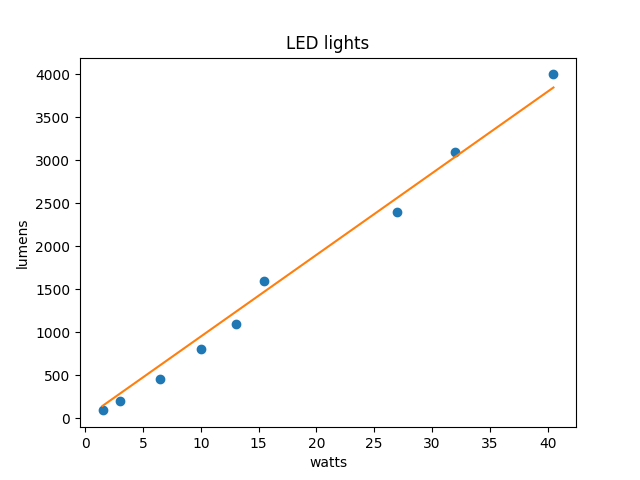
If you were to do a linear regression on the data you'd get a relation

lumens = a * watts + b

where the intercept term b is not zero. But this doesn't make sense: a light bulb that is turned off doesn't produce light, and it certainly doesn't produce negative light. [1]

You may be able fit the regression and ignore b; it's probably small. But what if you wanted to require that b = 0? Some regression software will allow you to specify zero intercept, and some will not. But it's easy enough to compute the slope a without using any regression software.

Let x be the vector of input data, the wattage of the LED bulbs. And let y be the corresponding light output in lumens. The regression line uses the slope a that minimizes

(a x - y)^2 = a^2 x x - 2a x y + y y.

Setting the derivative with respect to a to zero shows

a = x y / x x

Now there's more to regression than just line fitting. A proper regression analysis would look at residuals, confidence intervals, etc. But the calculation above was good enough to conclude that LED lights put out about 100 lumens per watt.

It's interesting that making the model more realistic, i.e. requiring b = 0, is either a complication or a simplification, depending on your perspective. It complicates using software, but it simplifies the math.

Related posts

• Best line to fit three points
• Logistic regression quick takes
• Linear regression and post quantum cryptography

[1] The orange line in the image above is the least squares fit for the model y = ax, but it's not quite the same line you'd get if you fit the model y = ax + b.

The post Fitting a line without an intercept term first appeared on John D. Cook.