Interpolation and the cotanc function

This weekend I wrote three posts related to interpolation:

• Compression and interpolation
• Bessel, Everett, and Lagrange interpolation
• Binomial coefficients with non-integer arguments

The first post looks at reducing the size of mathematical tables by switching for linear to quadratic interpolation. The immediate application is obsolete, but the principles apply to contemporary problems.

The second post looks at alternatives to Lagrange interpolation that are much better suited to hand calculation. The final post is a tangent off the middle post.

Tau and sigma functions

In the process of writing the posts above, I looked at Chambers Six Figure Mathematical Tables from 1964. There I saw a couple curious functions I hadn't run into before, functions the author called and .

(x) = x cot x
(x) = x csc x

So why introduce these two functions? The cotangent and cosecant functions have a singularity at 0, and so its difficult to tabulate and interpolate these functions. I touched on something similar in my recent post on interpolating the gamma function: because the function grows rapidly, linear interpolation gives bad results. Interpolating the log of the gamma function gives much better results.

Chambers tabulates (x) and (x) because these functions are easy to interpolate.

The cotanc function

I'll refer to Chambers' function as the cotanc function. This is a whimsical choice, not a name used anywhere else as far as I know. The reason for the name is as follows. The sinc function

sinc(x) = sin(x)/x

comes up frequently in signal processing, largely because it's the Fourier transform of the indicator function of an interval. There are a few other functions that tack a c onto the end of a function to indicate it has been divided by x, such as the jinc function.

The function tan(x)/x is sometimes called the tanc function, though this name is far less common than sinc. The cotangent function is the reciprocal of the tangent function, so I'm calling the reciprocal of the tanc function the cotanc function. Maybe it should be called the cotank function just for fun. For category theorists this brings up images of a tank that fires backward.

Practicality of the cotanc function

As noted above, the cotangent function function is ill-behaved near 0, but the cotanc function is very nicely behaved near 0. The cotanc function has singularities at non-zero multiples of but multiplying by x removes the singularity at 0.

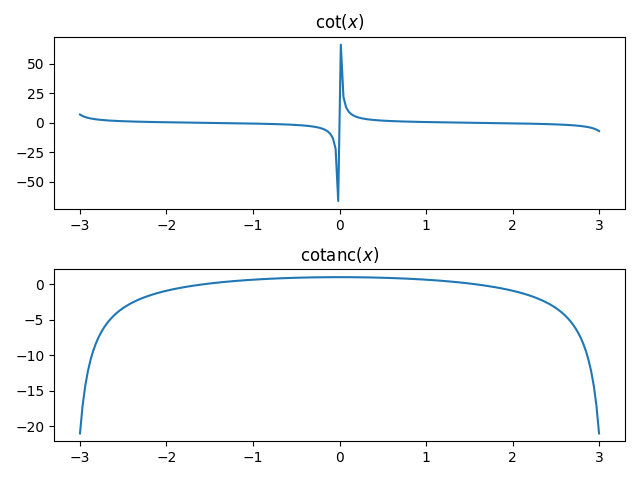
As noted here, interpolation error depends on the size of the derivatives of the function being interpolated. Since the cotanc function is flat and smooth, it has small derivatives and thus small interpolation error.

The post Interpolation and the cotanc function first appeared on John D. Cook.