Average number of divisors
Let d(n) be the number of divisors of an integer n. For example, d(12) = 6 because 12 is divisible by 1, 2, 3, 4, 6, and 12.
The function d varies erratically as the following plot shows.
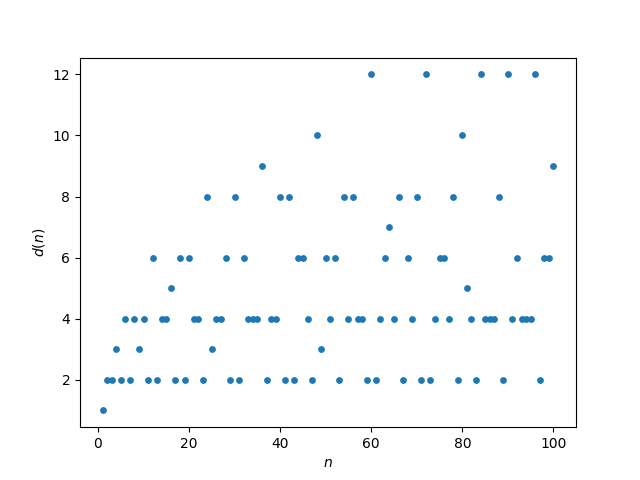
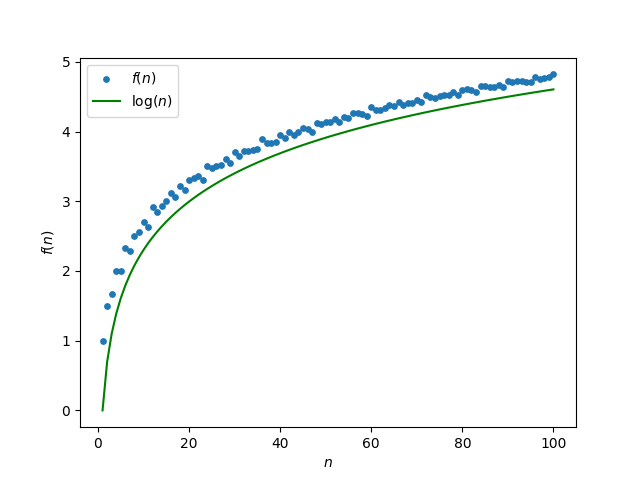
But if you take the running average of d
f(n) = (d(1) + d(2) + d(3) + ... + d(n)) / n
then this function is remarkably smoother.

Not only that, the function f(n) is asymptotically equal to log(n).
Incidentally, directly computing f(n) for n = 1, 2, 3, ..., N would be inefficient because most of the work in computingf(m) would be duplicated in computingf(m + 1). The inefficiency isn't noticeable for small N but matters more asN increases. It would be more efficient to iteratively compute f(n) by
f(n + 1) = (n f(n) + d(n + 1)) / (n + 1).
Asymptotics and citationsSeveral people have asked for a reference for the results above. I didn't know of one when I wrote the post, but thanks to reader input I now know that the result is due to Dirichlet. He proved that
f(n) = log(n) + 2 - 1 + o(1).
Here is the Euler-Mascheroni constant.
You can find Dirichlet's 1849 paper (in German) here. You can also find the result in Tom Apostle's book Introduction to Analytic Number Theory.
Related postsThe post Average number of divisors first appeared on John D. Cook.