Golden ellipse
A golden ellipse is an ellipse whose axes are in golden proportion. That is, the ratio of the major axis length to the minor axis length is the golden ratio = (1 + 5)/2.
Draw a golden ellipse and its inscribed and circumscribed circles. In other words draw the largest circle that can fit inside and the smallest circle outside that contains the ellipse.
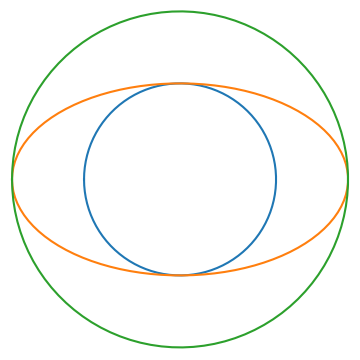
Then the area of the ellipse equals the area of the annulus bounded by the two circles. That is, the area of the green region

equals the area of the orange region.

The proof is straight forward. Let a be the semimajor axis andb the semiminor axis, with a = b.
Then the area of the annulus is
(a^2 - b^2) = b^2(^2 - 1).
The area of the ellipse is
ab = b^2.
The result follows because the golden ratio satisfies
^2 - 1 = .
Related postsThe post Golden ellipse first appeared on John D. Cook.