The glass disk game
The glass disk game is played on a grid. You have translucent colored glass disks you can either place on an edge or a vertex.
There are two kinds of disks that can be placed on an edge: blue or yellow. A vertex with a blue and yellow disk looks green.
There are two kinds of disks that can be placed on a vertex: red or white. A vertex with a red and white disk looks pink.
For this post we only need red disks. We may use white and pink in a future post.
The following rules tell you how you are allowed to add disks.
Rule 1If you have this configuration
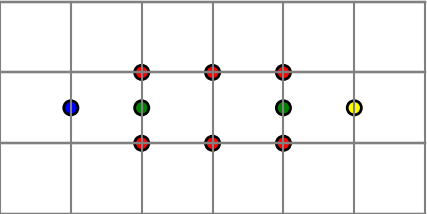
then you may add a green disk in the middle.
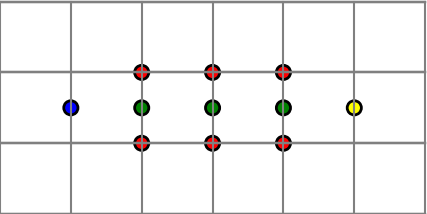
Mnemonic: Think of copying the blue and yellow dots on the end and placing them both in the middle.
Rule 2If you have this configuration
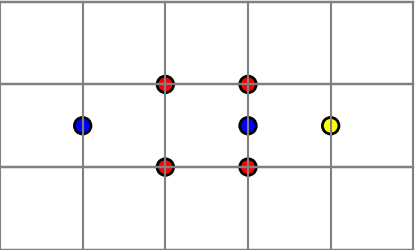
you may add a blue disk between the two blue disks.
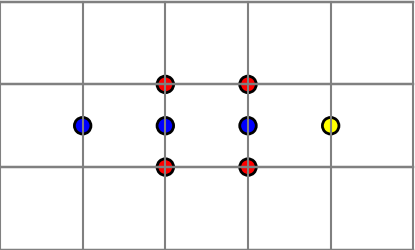
If you have this configuration
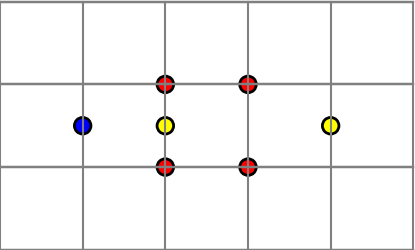
you may add a yellow disk between the two yellow disks.
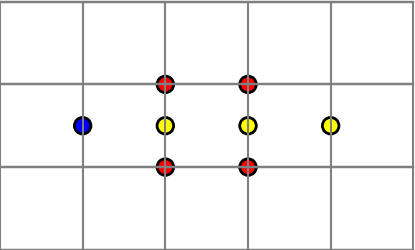
The rules above are all the rules of the game. You do not need to know any mathematics to play the game.
But the game does have a mathematical interpretation. The grid is a commutative diagram. A red disk means the horizontal diagram is exact at that vertex, i.e. the image of the function coming in from the left is the kernel of the function going out to the right.
A blue disk means a function is surjective (onto) and a yellow disk means a function is injective (one-to-one).
The diagram need not represent sets and functions. It could represent objects in a category along with morphisms. In that case blue disks represent epimorphisms and yellow disks monomorphisms.
Rule 1 is known as the five lemma. Rule 2 is called the four lemma.
The glass disk game is a pair of theorems in algebraic topology, or more generally homological algebra.
The post The glass disk game first appeared on John D. Cook.