Superhyperbola
An ellipse has equation
and a hyperbola has equation
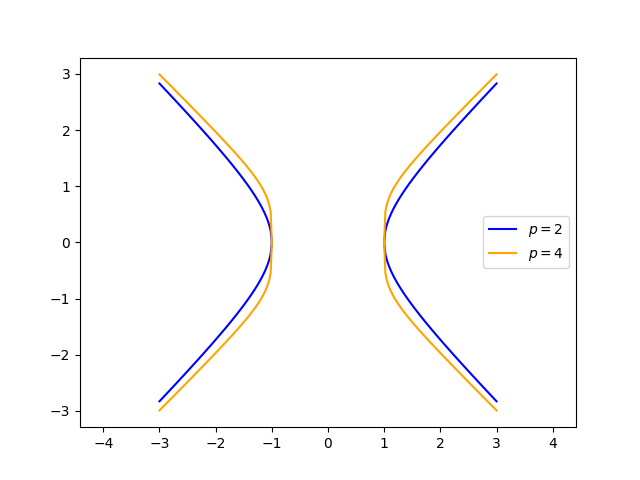
Similarly the superellipse has equation
and the superhyperbola
When p = 2, the absolute value signs are unnecessary and the superellipse and superhyperbola reduce to the ellipse and hyperbola respectively.
Increasingp makes the superellipse more like a rectangle. But unlike a rectangle with rounded corners, the change in curvature is continuous.
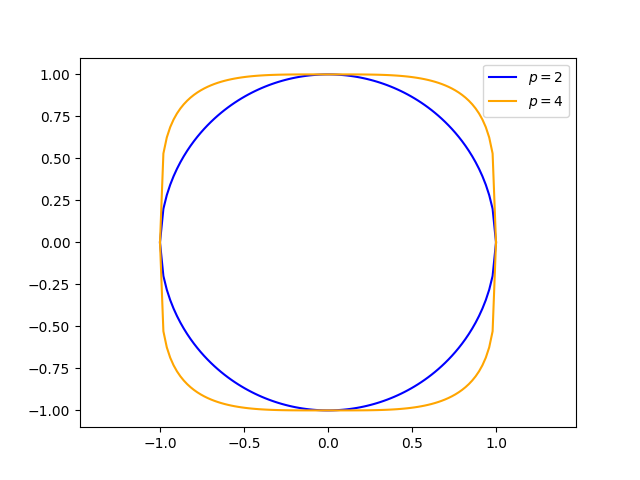
Increasingp makes the superhyperbola more blunt at the vertices.
The superellipse is a fairly well known variation on an ellipse. Even if you're not familiar the term, you've probably seen the shape. I give a couple examples here. The superhyperbola is the obvious analog of a superellipse, but the term is far less common. I'd never hear the term until yesterday.
It's not clear why the superellipse would be common and the superhyperbola obscure, but here's some speculation. First of all, the superellipse had an advocate, Piet Hein. If the superhyperbola has an advocate, he's not a very effective advocate.
The name is also off-putting: juxtaposing super andhyper sounds silly. The etymology makes sense, even if it sounds funny. Piet Hein used the prefixsuper- to refer to increasing the exponent from the usual value of 2. Its unfortunate thathyperbola begins with a root that is similar tosuper.
Related postsThe post Superhyperbola first appeared on John D. Cook.