Computing the Euler-Mascheroni Constant
The Euler-Mascheroni constant is defined as the limit
So an obvious way to try to calculate would be to evaluate the right-hand side above for large n. This turns out to not be a very good approach. Convergence is slow and rounding error accumulates.
A much better approach is to compute
It's not obvious that you can add the extra factor of in the log term, but you can: the right-hand sides of both equations above converge to , but the latter converges faster.
Here's a comparison of the two methods.
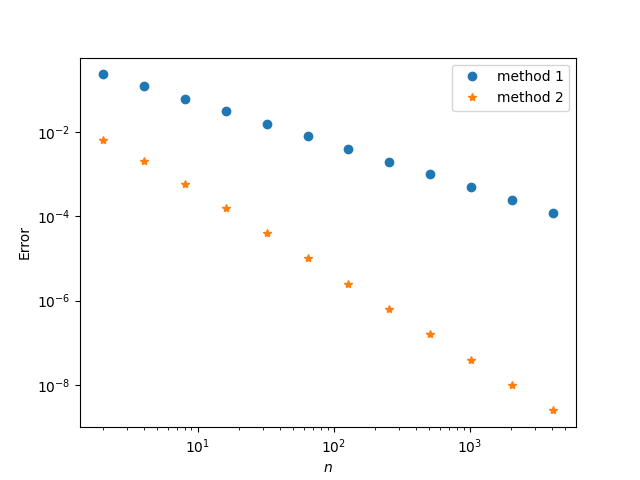
The error in the first method withn = 4000 is comparable to the error in the second method withn = 16.
Even though the second equation above is better for numerical evaluation, there are much more sophisticated approaches. And this brings us to y-cruncher, software that has been used to set numerous world records for computing various constants. A new record for computing the digits of was set a few weeks ago using y-cruncher. From the y-cruncher documentation:
Posts involving The post Computing the Euler-Mascheroni Constant first appeared on John D. Cook.Of all the things that y-cruncher supports, the Euler-Mascheroni Constant is the slowest to compute and by far the most difficult to implement. ...
The Euler-Mascheroni Constant has a special place in y-cruncher. It is one of the first constants to be supported (even before Pi) and it is among the first for which a world record was set using y-cruncher. As such, y-cruncher derives its name from the gamma symbol for the Euler-Mascheroni Constant.