A recipe for creating random fractals

Last week I gave an example of a randomly generated fractal and mentioned that it was a particularly special case of a more general algorithm for generating similar fractals found in [1]."

Here's the general pattern. First, create a non-singular matrixM with integer entries and let k be the determinant ofM.

LetP be the parallelogram spanned by the columns ofM. Choose a set of column vectors r_i for i = 1, 2, 3, ..., k from the two columns ofM and from the interior ofP.

Pick a random starting vectorv then iterate

v =M^-1v +r_i

wherei is chosen at random on each iterations.

Here's an example suggested as an exercise in [2]. We start with

and look at the parallelogram spanned by the columns of M.

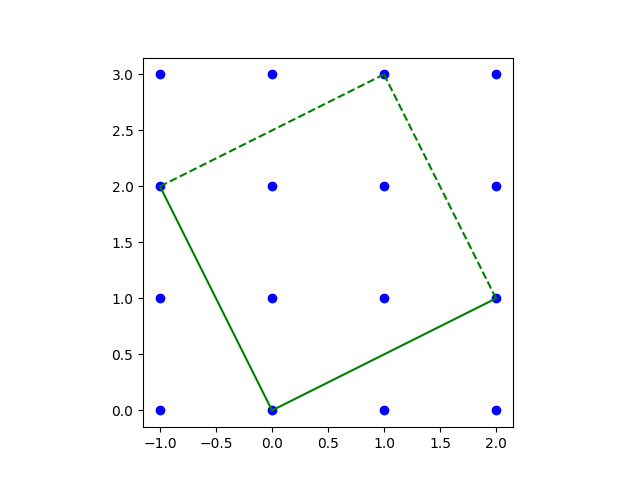
NB: The initial version of this post had an error in the grid, which led to an error in the code, and produced a different fractal.

Then the algorithm described above is implemented in the following Python code.

import numpy as npimport matplotlib.pyplot as pltA = np.linalg.inv(np.array([[2, -1], [1, 2]]))R = np.array([[2, -1, 0, 1, 1], [1, 2, 2, 2, 1]])v = np.random.random(size=2)for _ in range(100000): i = np.random.choice([0, 1, 2, 3, 4]) v = np.dot(A, v) + R[:, i] plt.plot(v[0], v[1], 'bo', markersize=1)plt.gca().set_aspect("equal")plt.show()

This produces the following fractal.

[1] Darst, Palagallo, and Price. Fractal Tilings in the Plane. Mathematics Magazine [71]:1, 1998.

[2] Lorelei Koss, Fractal Rep-tiles and Geometric Series. Math Horizons. Vol 30, Issue 1, September 2022.

The post A recipe for creating random fractals first appeared on John D. Cook.