Knuth’s Twindragon
A few days ago I wrote about a random process that creates a fractal known as the Twin Dragon. This post gives a deterministic approach to create the same figure.
As far as I can tell, the first reference to this fractal is in a paper by Davis and Knuth in the Journal of Recreational Mathematics from 1970. Unfortunately this journal is out of print and hard or impossible to find online [1]. Knuth presents the twindragon (one word, lowercase) fractal in TAOCP Vol 2, page 206.
Knuth defines the twindragon via numbers base b = 1 - i. Every complex number can be written in the form
where the digits" ak are either 0 or 1.
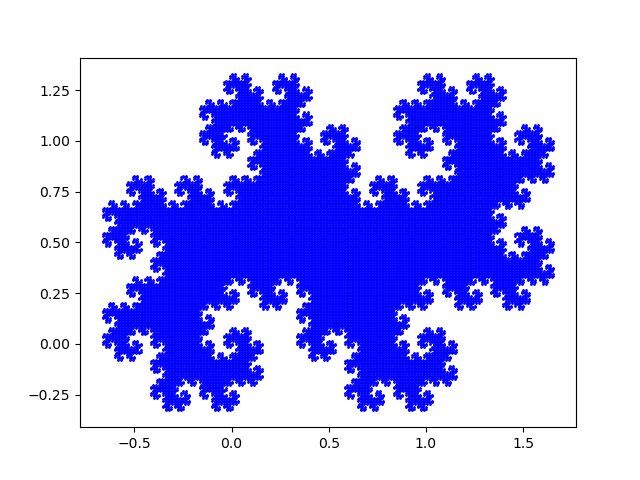
The twindragon fractal is the set of numbers that only have non-zero digits to the right of the decimal point, i.e. numbers of the form
I implemented this in Python as follows.
import matplotlib.pyplot as pltfrom itertools import productfor bits in product([0, 1], repeat=15): z = sum(a*(1-1j)**(-k) for k, a in enumerate(bits)) plt.plot(z.real, z.imag, 'bo', markersize=1)plt.show()
This produced the image below.
[1] If you can find an archive of Journal of Recreational Mathematics, please let me know.
The post Knuth's Twindragon first appeared on John D. Cook.