Differential equation on a doughnut

Here's a differential equation from [1] that's interesting to play with.

Even though it's a nonlinear system, it has a closed-form solution, namely

where (a,b,c) is the solution att = 0 and = 1 + a^2 + b^2 + c^2.

The solutions lie on the torus (doughnut). Ifm andn are coprime integers then the solutions form a closed loop. If the ratiom/n is not rational then the solutions are dense on the torus.

Here's an example with parametersa = 1, b = 1, c = 3, m = 3, and n = 5.

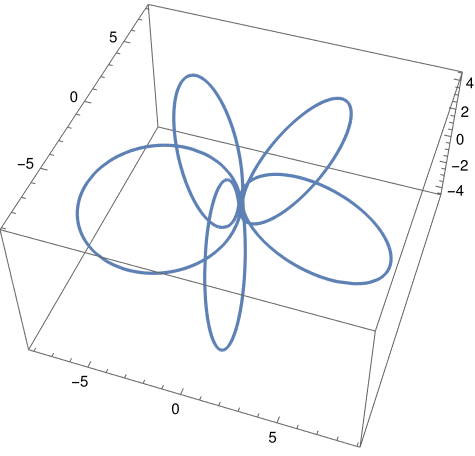
And now with parameters a = 1, b = 1, c = 0.3, m = 4, and n = 5.

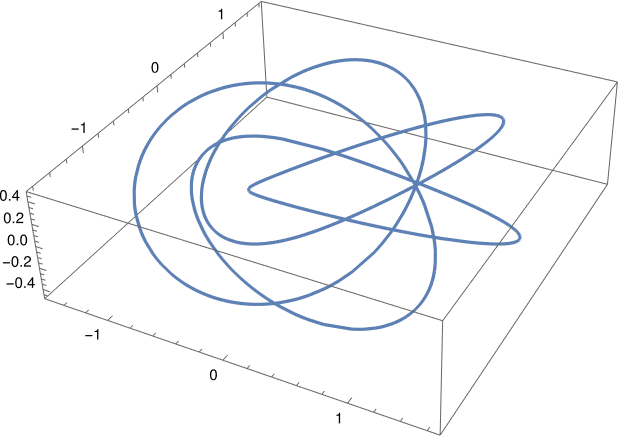
And finally with parameters a = 1, b = 1, c = 0.3, m = , and n = 5.

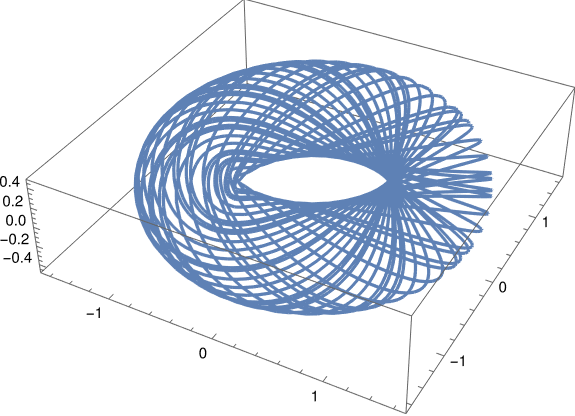
Note that when m = 2 and n = 3 the trajectory traces out a trefoil knot.

Related posts

• Oscilliatory differential equations
• Stiff differential equations
• Life lessons from differential equations

[1] Richard Parris. A Three-Dimensional System with Knotted Trajectories. The American Mathematical Monthly, Vol. 84, No. 6 (Jun. - Jul., 1977), pp. 468-469

The post Differential equation on a doughnut first appeared on John D. Cook.