Inverting matrices and bilinear functions

The inverse of the matrix

is the matrix

assumingad - bc 0.

Also, the inverse of the bilinear function (a.k.a. Mobius transformation)

is the function

again assumingad - bc 0.

The elementary takeaway is that here are two useful equations that are similar in appearance, so memorizing one makes it easy to memorize the other. We could stop there, but let's dig a little deeper.

There is apparently an association between 2 * 2 matrices and Mobius transformations

This association is so strong that we can use it to compute the inverse of a Mobius transformation by going to the associated matrix, inverting it, and going back to a Mobius transformation. In diagram form, we have the following

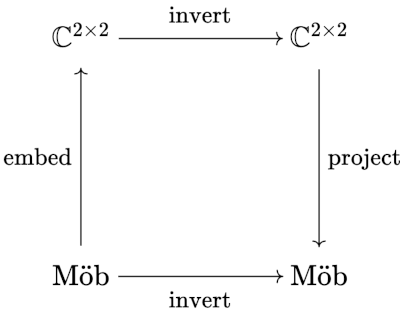
Now there are a few lose ends. First of all, we don't really have a map between Mobius transformations and matrices per se; we have a map between a particular representation of a Mobius transformation and a 2 * 2 matrix. If we multiplieda,b,c, andd in a Mobius transformation by 10, for example, we'd still have the same transformation, just a different representation, but it would go to a different matrix.

What we really have a map between Mobius transformations and equivalence classes of invertible matrices, where two matrices are equivalent if one is a non-zero multiple of the other. If we wanted to make the diagram above more rigorous, we'd replace ^2*2 with PL(2, ), linear transformations on the complex projective plane. In sophisticated terms, our map between Mobius transformations and matrices is an isomorphism between automorphisms of the Riemann sphere and PL(2, ).

Mobius transformations act a lot like linear transformations because they are linear transformations, but on the complex projective plane, not on the complex numbers. More on that here.

The post Inverting matrices and bilinear functions first appeared on John D. Cook.