An ancient generalization of the Pythagorean theorem

Apollonius of Perga (c. 262 BC - c. 190 BC) discovered a theorem that generalizes the Pythagorean theorem but isn't nearly as well known.

Let ABC be a general triangle, and let D be the midpoint of the segment AB. Leta be the length of the side opposite A andb the length of the side opposite B. Letm be the length of AD andh the length of the mediant, the line CD.

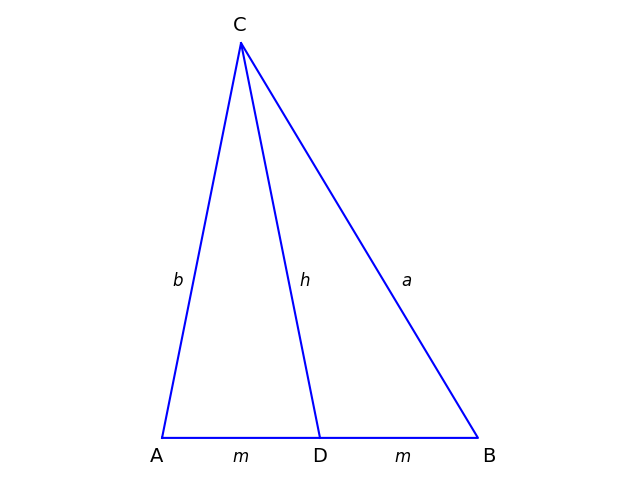
Apollonius's theorem says

a^2 + b^2 = 2(m^2 + h^2).

To see that this is a generalization of the Pythagorean theorem, apply Apollonius' theorem to an isosceles triangle. Nowa =b and ACD is a right triangle.

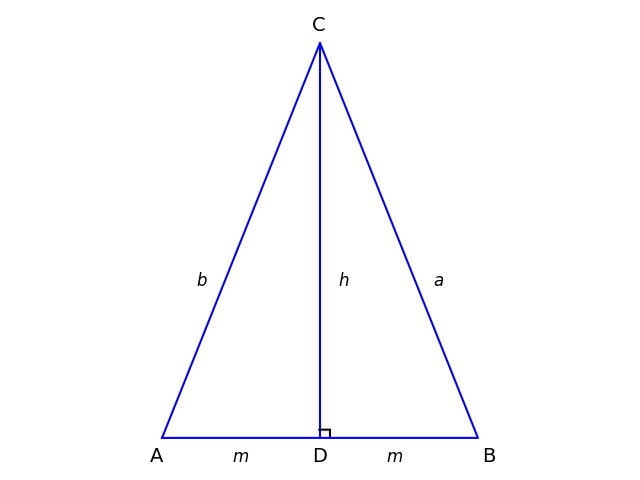
Apollonius' theorem says

2b^2 = 2m^2 + 2h^2

which is the Pythagorean theorem applied to ACD with each term doubled.

The post An ancient generalization of the Pythagorean theorem first appeared on John D. Cook.