Hyperbolic metric

One common model of the hyperbolic plane is the Poincare upper half plane . This is the set of points in the complex plane with positive imaginary part. Straight lines are either vertical, a set of points with constant imaginary part, or arcs of circles centered on the real axis. The real axis is not part of . From the perspective of hyperbolic geometry these are ideal parts, infinitely far away, and not part of the plane itself.

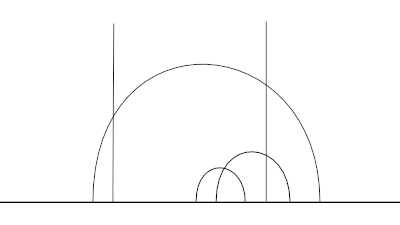
We can define a metric on as follows. To find the distance between two pointsu and v, draw a line between the two points, and let a andb be the ideal points at the end of the line. By a line we mean a line as defined in the geometry of , what we would see from our Euclidean perspective as a half circle or a vertical line. Then the distance betweenu andv is defined as the absolute value of the log of the cross ratio (u, v; a,b).

Cross ratios are unchanged by Mobius transformations, and so Mobius transformations are isometries.

Another common model of hyperbolic geometry is the Poincare disk. We can use the same metric on the Poincare disk because the Mobius transformation

maps the upper half plane to the unit disk. This is very similar to how the Smith chart is created by mapping a grid in the right half plane to the unit disk.

Update: See the next post for four analytic expressions for the metric, direct formulas involvingu andv but not the ideal pointsa andb.

The post Hyperbolic metric first appeared on John D. Cook.