Rolling n-sided dice to get at least n

Say you have a common 6-sided die and need to roll it until the sum of your rolls is at least 6. How many times would you need to roll?

If you had a 20-sided die and you need to roll for a sum of at least 20, would that take more rolls or fewer rolls on average?

According to [1], the expected number of rolls of an n-sided dice for the sum of the rolls to be n or more equals

So for a 6-sided die, the expected number of rolls is (7/6)⁵ = 2.1614.

For a 20-sided die, the expected number of rolls is (21/20)¹⁹ = 2.5270.

The expected number of rolls is an increasing function ofn, and it converges toe.

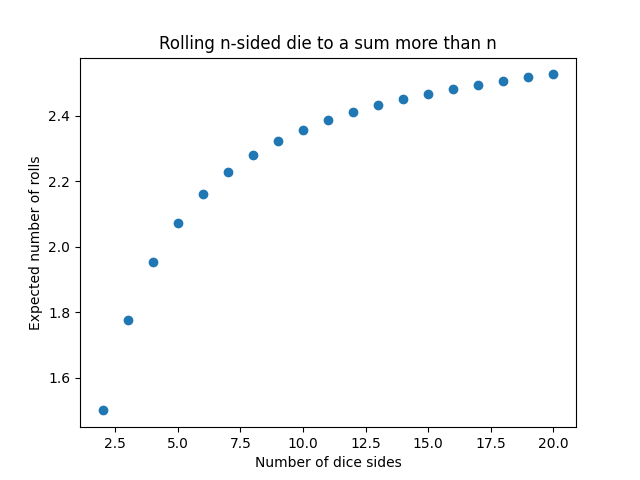
Here's a little simulation script for the result above.

from numpy.random import randintdef game(n): s = 0 i = 0 while s < n: s += randint(1, n+1) i += 1 return iN = 1_000_000s = 0n = 20for _ in range(N): s += game(n)print(s / N)

This produced 2.5273.

[1] Enrique Trevino. Expected Number of Dice Rolls for the Sum to Reach n. American Mathematical Monthly, Vol 127, No. 3 (March 2020), p. 257.

The post Rolling n-sided dice to get at least n first appeared on John D. Cook.