Matrix Pythagorean Triples

A Pythagorean triple is a list of positive integers (a, b, c) such that a² + b² = c². Euclid knew how to find all Pythagorean triples: pick two positive integers m and n with m > n and let

a = m² - n², b = 2mn, c = m² + n².

Now what if we look at matrices with integer entries such that A² + B² = C²? Are there any? Yes, here's an example:

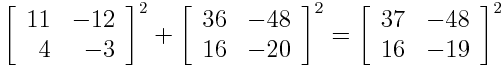
How can you find matrix-valued Pythagorean triples? One way is to create diagonal matrices with Pythagorean triple integers. Take a list of n Pythagorean triples (a_i, b_i, c_i) and create diagonal matrices A, B, and C with the a_i along the diagonal of A, b_i along the diagonal of B, and c_i along the diagonal of C.

But that seems cheap. We're really not using any properties of matrix multiplication other than the fact that you can square a diagonal matrix by squaring its elements. One way to create more interesting matrix Pythagorean triples is to start with the diagonal matrices described above and conjugate them by some matrix Q with integer entries such that Q^-1 also has integer entries. Here's why that works:

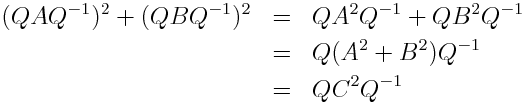
The example above was created by starting with the Pythagorean triples (3, 4, 5) and (5, 12, 13), creating diagonal matrices, and conjugating by

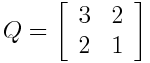
This gives a way to create lots of matrix Pythagorean triples, but there may triples that this procedure leaves out.

Related: Approximations with Pythagorean triangles