Chaos and the double dendulum
by Mark Frauenfelder from on (#13H4A)

Brian, a graduate student of Applied Mathematics at Columbia University, has a Tumblr called Fouriest Series where he posts his math and physics visualizations. His explanations are clearly written. He also provides the Mathematica code he used to create his animations.From his post about chaos and double pendulums:
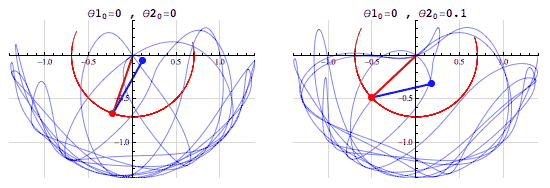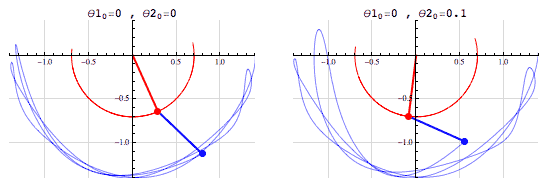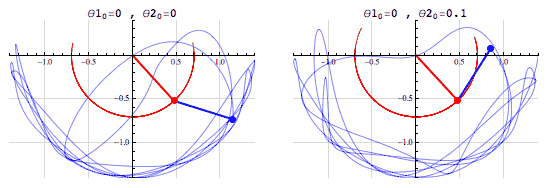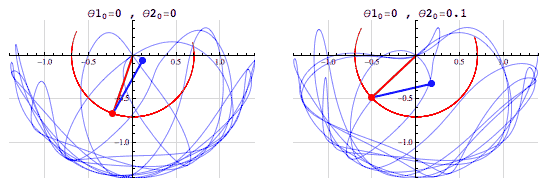
Summarized by mathematician Edward Lorenz, "Chaos [is] when the present determines the future, but the approximate present does not approximately determine the future."There's an important distinction to make between a chaotic system and a random system. Given the starting conditions, a chaotic system is entirely deterministic. A random system, on the other hand, is entirely non-deterministic, even when the starting conditions are known. That is, with enough information, the evolution of a chaotic system is entirely predictable, but in a random system there's no amount of information that would be enough to predict the system's evolution.The simulations above show two slightly different initial conditions for a double pendulum - an example of a chaotic system. In the left animation both pendulums begin horizontally, and in the right animation the red pendulum begins horizontally and the blue is rotated by 0.1 radians (a 5.73) above the positive x-axis. In both simulations, all of the pendulums begin from rest.
[via]