Correlation of two sine waves

What is the correlation of two sine waves that differ in phase? The result itself is interesting, and the calculation along the way shows tricks to avoid calculating integrals.

The correlation of two periodic signals, f and g, is

where the integral is over a period of the two functions. For functions known at discrete points this would be a sum rather than an integral, but in this case we have continuous signals so we integrate.

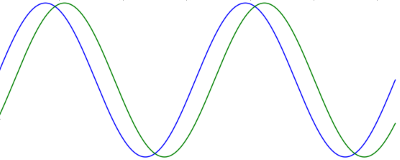
In our case the two functions are f(t) = sin(t) and g(t) = sin(t + I) and the integrals are over [0, 2I]. Both functions have average value 0, so the I1/4 terms go away.

We use a trig identity to expand the numerator:

In our case I₁ = t and I₂ = t + I and so the numerator becomes

The first part of the integral is integrating a constant (with respect to t) and so becomes the constant times the length of the integration range. The second part of the integral is zero because it is integrating a cosine over two periods.

Now for the denominator. Over a full period, sin²(t) and cos²(t) take on the same values, just shifted. So the integral of sin²(t) is half the integral of sin²(t) + cos²(t) = 1. Therefore

and the same argument shows that the integral of sin²(t + I) is also I. So our correlation is simply cos I: the correlation of two out-of-phase sine waves is the cosine of their phase difference. It may be a little surprising that it works out to be so simple, but the result makes sense. When I = 0, or any multiple of 2I, the waves are identical and so the correlation should be 1. When I = I, or an odd multiple of I, the two waves are perfectly out of phase, and so the correlation should be -1. In between these extremes the correlation oscillates, in fact it is a cosine.