Bessel series for a constant

Fourier series express functions as a sum of sines and cosines of different frequencies. Bessel series are analogous, expressing functions as a sum of Bessel functions of different orders.

Fourier series arise naturally when working in rectangular coordinates. Bessel series arise naturally when working in polar coordinates.

The Fourier series for a constant is trivial. You can think of a constant as a cosine with frequency zero.

The Bessel series for a constant is not as simple, but more interesting. Here we have

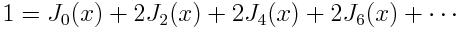
Since

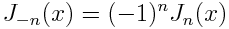
we can write the series above more symmetrically as

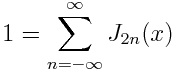
Related posts:

• Energy in FM signals
• Maximum principles for initial value problems
• Relationships between Bessel functions