Golden powers are nearly integers

This morning I was reading Terry Tao's overview of the work of Yves Meyer and ran across this line:

The powers I, I², I³, " of the golden ratio lie unexpectedly close to integers: for instance, I¹¹ = 199.005" is unusually close to 199.

I'd never heard that before, so I wrote a little code to see just how close golden powers are to integers.

Here's a plot of the difference between Iⁿ and the nearest integer:

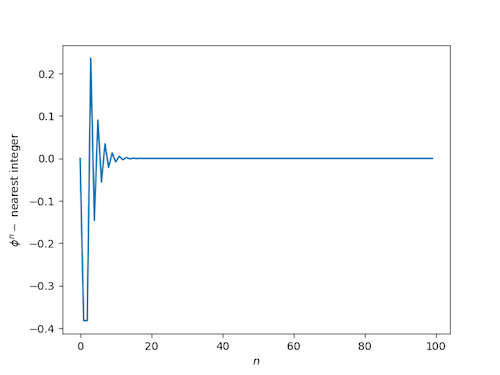
(Note that if you want to try this yourself, you need extended precision. Otherwise you'll get strange numerical artifacts once Iⁿ is too large to represent exactly.)

By contrast, if we make the analogous plot replacing I with I we see that the distance to the nearest integer looks like a uniform random variable:

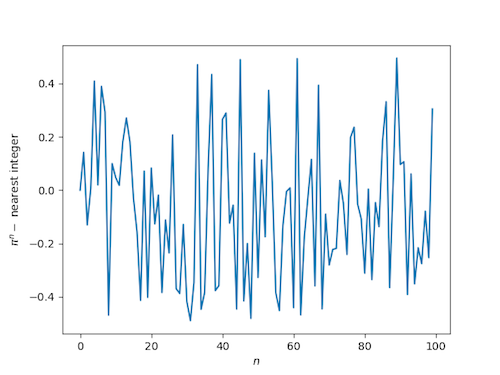
The distance from powers of I to the nearest integer decreases so fast that cannot see it in the graph for moderate sized n, which suggests we plot the difference on the log scale. (In fact we plot the log of the absolute value of the difference since the difference could be negative and the log undefined.) Here's what we get:

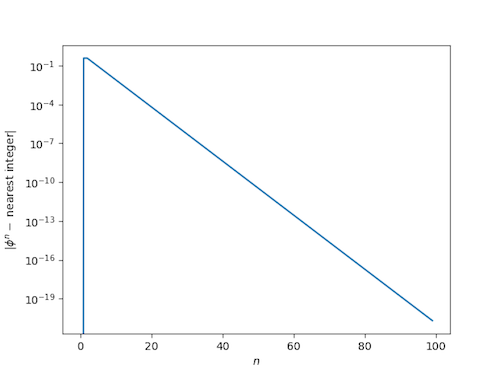
After an initial rise, the curve is apparently a straight line on a log scale, i.e. the absolute distance to the nearest integer decreases almost exactly exponentially.

Related posts:

• Imaginary gold
• Power method and Fibonacci ratios
• Fibonacci numbers and numerical integration
• Applied number theory