Plastic powers
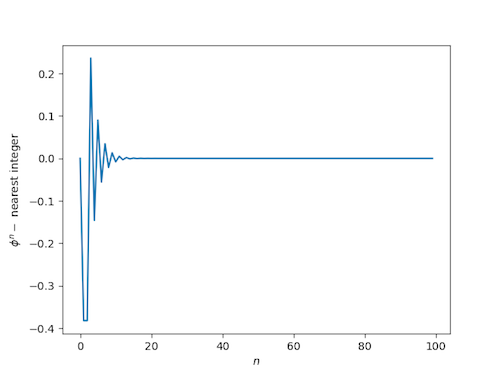
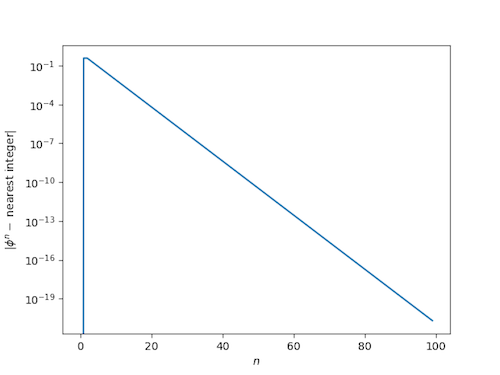
Last week I wrote a blog post showing that powers of the golden ratio are nearly integers. Specifically, the distance from In to the nearest integer decreases exponentially as n increases. Several people pointed out that the golden constant is a Pisot number, the general class of numbers whose powers are exponentially close to integers.
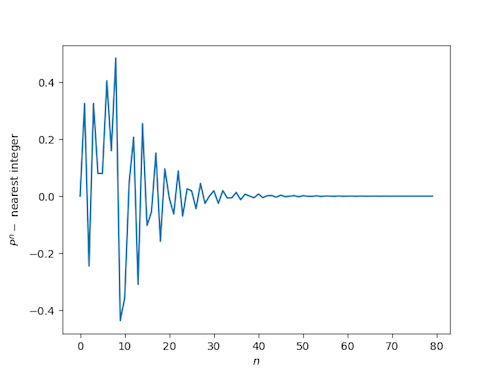
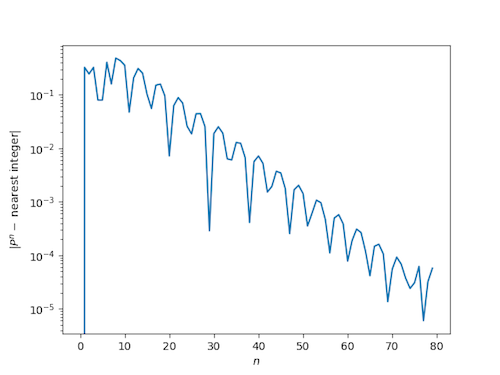
The so-called plastic constant P is another Pisot number, in fact the smallest Pisot number. P is the real root of x3 - x - 1 = 0.

Because P is a Pisot number, we know that its powers will be close to integers, just like powers of the golden ratio, but the way they approach integers is more interesting. The convergence is slower and less regular.
We will the first few powers of P, first looking at the distance to the nearest integer on a linear scale, then looking at the absolute value of the distance on a logarithmic scale.
As a reminder, here's what the corresponding plots looked like for the golden ratio.