Distribution of zeros of the Riemann zeta

A recent video by Quanta Magazine says that the eigenvalues of random matrices and the zeros of the Riemann zeta function appear to have the same distribution.

I assume by "random matrices" the video is referring specifically to Gaussian orthogonal ensembles. [Update: See the first comment below for more details. You need some assumptions on the distribution-fat tails are out-but you don't need to assume a GOE.]

By zeros of the Riemann zeta function, they mean the imaginary parts of the zeros in the critical strip. You can download the first 100,000 zeros of the Riemann zeta function here. So, for example, the first zero is 14.134725142, which actually means 0.5 + 14.134725142 i.

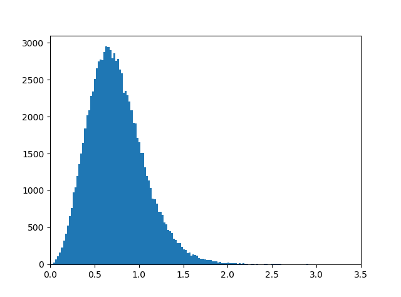
Here's the histogram of random matrix eigenvalues from my previous post:

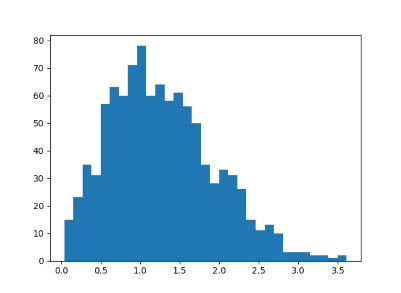
And here's a histogram of the spacing between the first two thousand zeros of the Riemann zeta function:

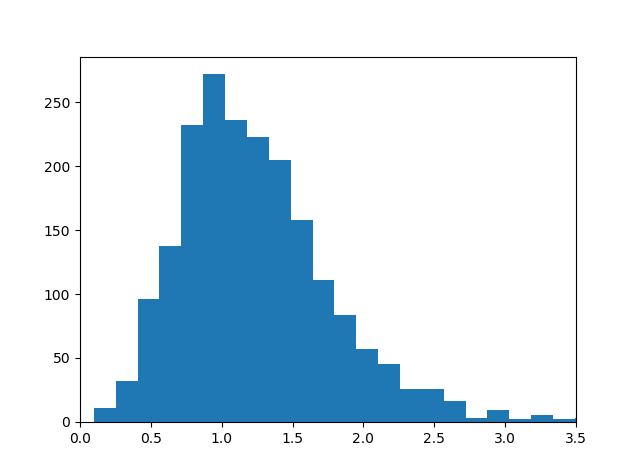
The distribution of random matrix eigenvalues is known exactly. I believe the distribution of the Riemann zeta function zeros is conjectural but persuasive. Here's a plot using the first 100,000 zeros.