Lissajous curves and knots

Suppose that over time the x and y coordinates of a point are both given by a harmonic oscillator, i.e.

x(t) = cos(n_xt + I_x)
y(t) = cos(n_yt + I_y)

Then the resulting path is called a Lissajous curve.

If you add a z coordinate also given by harmonic oscillator

z(t) = cos(n_zt + I_z)

then the result is a Lissajous knot. This means that if we project a Lissajous knot onto a coordinate plane, we get a Lissajous curve.

For example, here is a Lissajous knot. See the code at the bottom for parameter details.

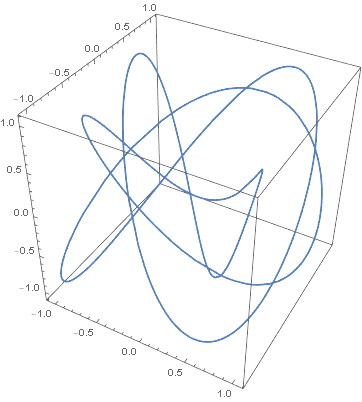
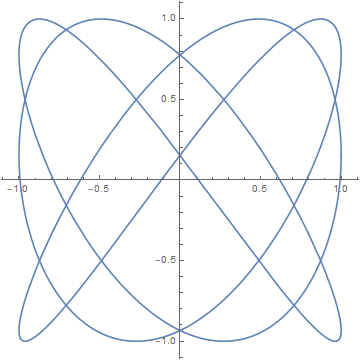
Here are its projections onto the xy plane,

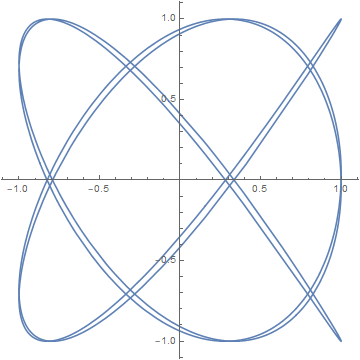
the yz plane,

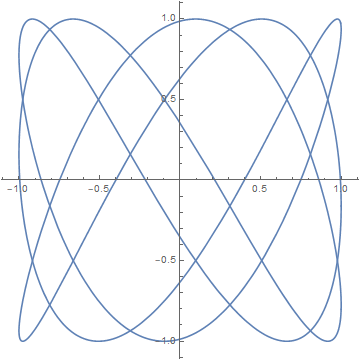
and the xz plane.

If you've ever seen an oscilloscope, you may have seen Lissajous curves on its screen.

In order to get a knot, we require that the frequencies, the n's, are pairwise relatively prime. We also require that the curve not intersect itself, which imposes a constraint on the phases, the I's, as well.

Last week I used torus knots as an example of a family of knots. The Lissajous knots are a distinct family of knots: no torus knot is also a Lissajous knot.

Here's the Mathematica code to produce the images above.

x[t_] := Cos[3 t]y[t_] := Cos[4 t + Sqrt[2]]z[t_] := Cos[5 t + Sqrt[3]]ParametricPlot3D[{x[t], y[t], z[t]}, {t, 0, 2 Pi}]ParametricPlot[{x[t], y[t]}, {t, 0, 2 Pi}]ParametricPlot[{y[t], z[t]}, {t, 0, 2 Pi}]ParametricPlot[{x[t], z[t]}, {t, 0, 2 Pi}]