Solving Van der Pol equation with ivp_solve

Van der Pol's differential equation is

The equation describes a system with nonlinear damping, the degree of nonlinearity given by I1/4. If I1/4 = 0 the system is linear and undamped, but as I1/4 increases the strength of the nonlinearity increases. We will plot the phase portrait for the solution to Van der Pol's equation in Python using SciPy's new ODE solver ivp_solve.

The function ivp_solve does not solve second-order systems of equations directly. It solves systems of first-order equations, but a second-order differential equation can be recast as a pair of first-order equations by introducing the first derivative as a new variable.

Since y is the derivative of x, the phase portrait is just the plot of (x, y).

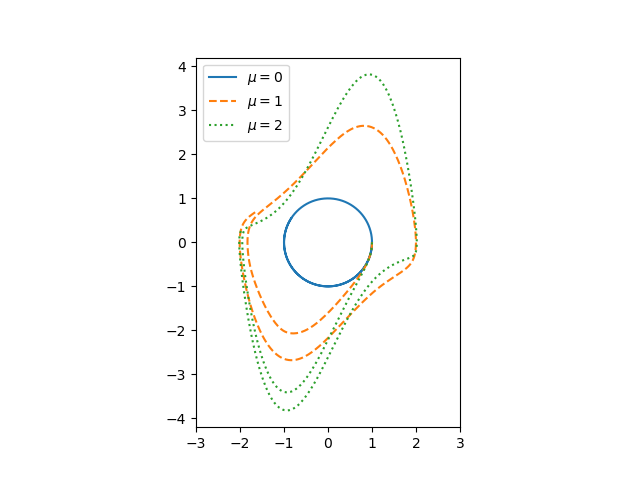
If I1/4 = 0, we have a simple harmonic oscillator and the phase portrait is simply a circle. For larger values of I1/4 the solutions enter limiting cycles, but the cycles are more complicated than just circles. These limiting cycles are periodic attractors: every non-trivial solution converges to the limit cycle.

Here's the Python code that made the plot.

from scipy import linspacefrom scipy.integrate import solve_ivpimport matplotlib.pyplot as pltdef vdp(t, z): x, y = z return [y, mu*(1 - x**2)*y - x]a, b = 0, 10mus = [0, 1, 2]styles = ["-", "--", ":"]t = linspace(a, b, 500)for mu, style in zip(mus, styles): sol = solve_ivp(vdp, [a, b], [1, 0], t_eval=t) plt.plot(sol.y[0], sol.y[1], style) # make a little extra horizontal room for legendplt.xlim([-3,3]) plt.legend([f"$\mu={m}$" for m in mus])plt.axes().set_aspect(1)

To plot the solutions as a function of time, rather than plotting phase portraits, change the line

 plt.plot(sol.y[0], sol.y[1], style)

to

 plt.plot(sol.t, sol.y[0], style)

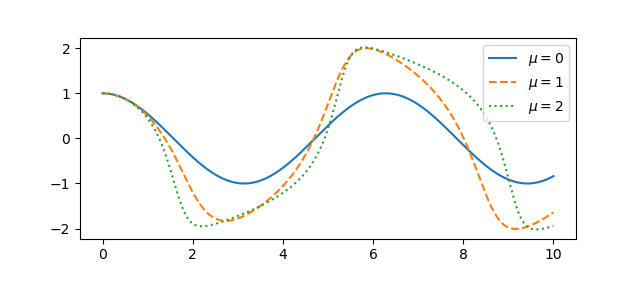
and comment out the line setting xlim This gives the following plot.

• Calculation periods of Van der Pol oscillations
• The other butterfly effect
• Linear mechanical vibrations