Cobweb plots
Cobweb plots are a way of visualizing iterations of a function.
For a function f and a starting point x, you plot (x, f(x)) as usual. Then since f(x) will be the next value of x, you convert it to an x by drawing a horizontal line from (x, f(x)) to (f(x), f(x)). In other words, you convert the previous y value to an x value by moving to where a horizontal line intersects the line y = x. Then you go up from the new x to f applied to the new x. The Python code below makes this all explicit.
Update: I made a couple changes after this post was first published. I added the dotted line y = x to the plots, and I changed the aspect ratio from the default to 1 to make the horizontal and vertical scales the same.
import matplotlib.pyplot as plt from scipy import cos, linspace def cobweb(f, x0, N, a=0, b=1): # plot the function being iterated t = linspace(a, b, N) plt.plot(t, f(t), 'k') # plot the dotted line y = x plt.plot(t, t, "k:") # plot the iterates x, y = x0, f(x0) for _ in range(N): fy = f(y) plt.plot([x, y], [y, y], 'b', linewidth=1) plt.plot([y, y], [y, fy], 'b', linewidth=1) x, y = y, fy plt.axes().set_aspect(1) plt.show() plt.close()
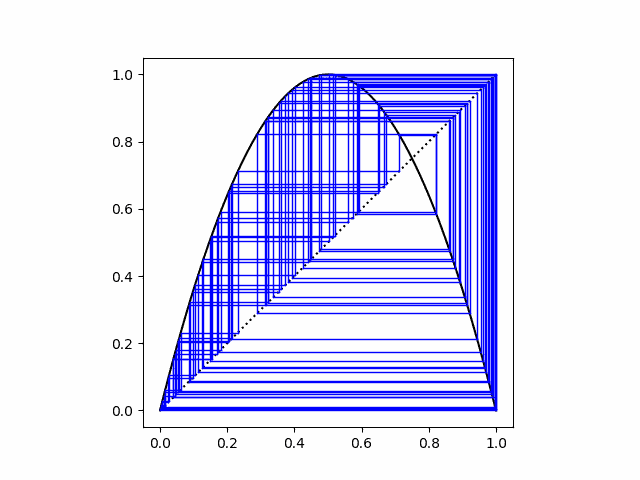
The plot above was made by calling
cobweb(cos, 1, 20)
to produce the cobweb plot for 20 iterations of cosine starting with x = 1. There's one fixed point, and the cobweb plot spirals into that fixed point.
Next let's look at several iterations of the logistic map f(x) = rx(1 - x) for differing values of r.
# one fixed point cobweb(lambda x: 2.9*x*(1-x), 0.1, 100) # converging to two-point attractor cobweb(lambda x: 3.1*x*(1-x), 0.1, 100) # starting exactly on the attractor cobweb(lambda x: 3.1*x*(1-x), 0.558, 100) # in the chaotic region. cobweb(lambda x: 4.0*x*(1-x), 0.1, 100)
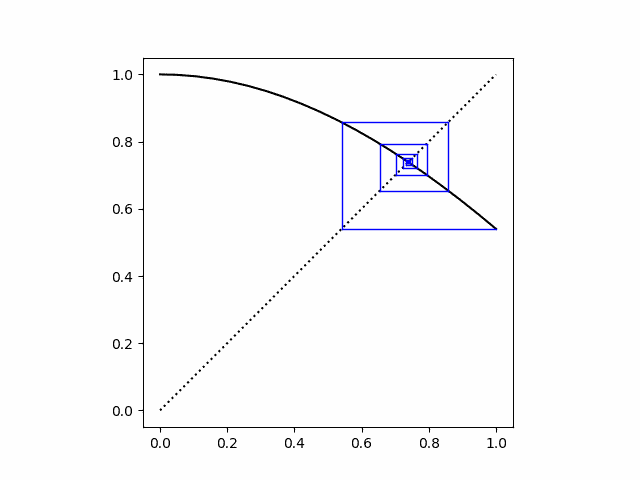
The logistic map also has one stable fixed point if r a 3. In the plot below, r = 2.9.
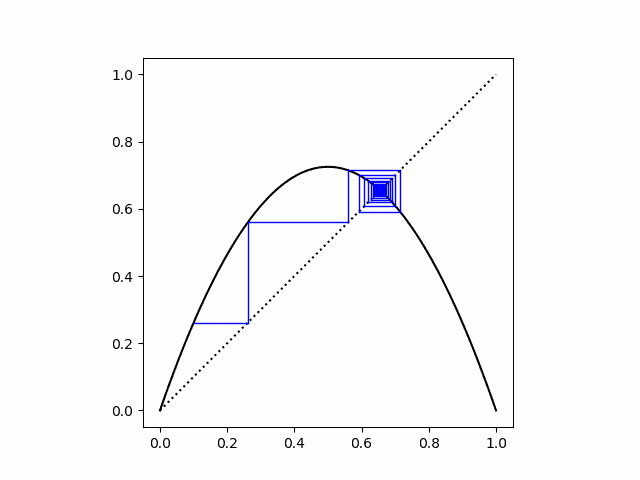
Next we set r = 3.1. We start at x = 0.1 and converge to the two attractor points.
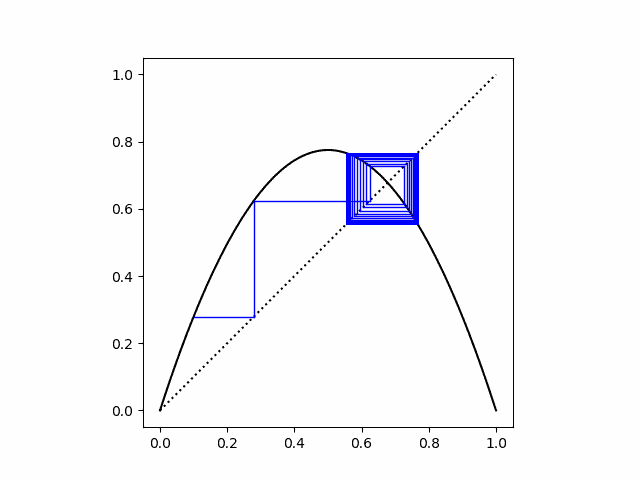
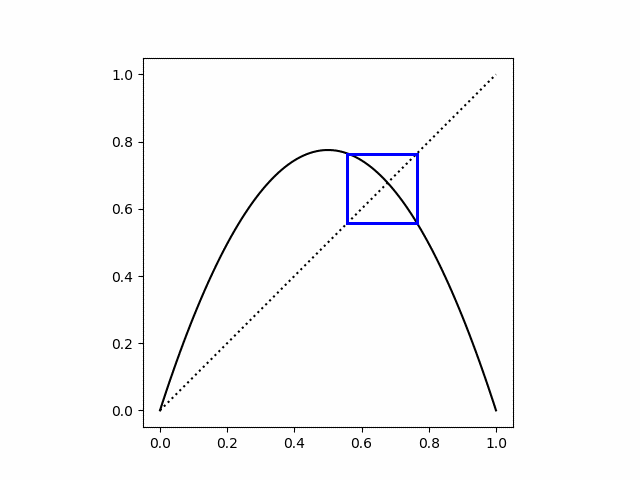
If we start exactly on one of the attractor points the cobweb plot is simply a square.
Finally, when we set r = 4 we're in the chaotic region.