NASA’s favorite ODE solver

John

from John D. Cook on 2020-06-16 22:19 (#54PZ8)

NASA's Orbital Flight Handbook, published in 1963, is a treasure trove of technical information, including a section comparing the strengths and weaknesses of several numerical methods for solving differential equations.

The winner was a predictor-corrector scheme known as Gauss-Jackson, a method I have not heard of outside of orbital mechanics, but one apparently particularly well suited to NASA's needs.

The Gauss-Jackson second-sum method is strongly recommended for use in either Encke or Cowell [approaches to orbit modeling]. For comparable accuracy, it will allow step-sizes larger by factors of four or more than any of the forth order methods. ... As compared with unsummed methods of comparable accuracy, the Gauss-Jackson method has the very important advantage that roundoff error growth is inhibited. ... The Gauss-Jackson method is particularly suitable on orbits where infrequent changes in the step-size are necessary.

Here is a table summarizing the characteristics of each of the solvers.

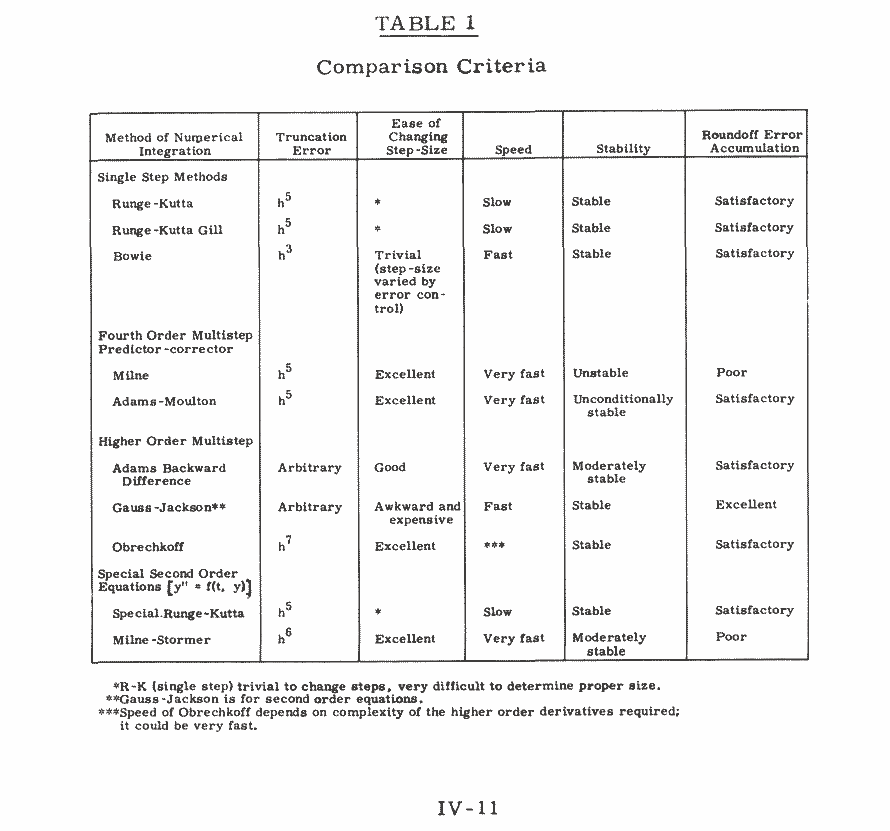
Notice that Gauss-Jackson is the only method whose roundoff error accumulation is described as excellent."

A paper from 2004 [1] implies that the Gauss-Jackson method was still in use at NASA at the time of writing.

The Gauss-Jackson multi-step predictor-corrector method is widely used in numerical integration problems for astrodynamics and dynamical astronomy. The U.S. space surveillance centers have used an eighth-order Gauss-Jackson algorithm since the 1960s.

I could imagine a young hotshot explaining to NASA why they should use some other ODE solver, only to be told that the agency had already evaluated the alternatives half a century ago, and that the competitors didn't have the same long-term accuracy.

Source	RSS or Atom Feed
Feed Location	http://feeds.feedburner.com/TheEndeavour?format=xml
Feed Title	John D. Cook
Feed Link	https://www.johndcook.com/blog