Life, part 31

Today we will finish off our implementation of Hensel's QuickLife algorithm, rewritten in C#. Code for this episode is here.

Last time we saw that adding change tracking is an enormous win, but we still have not got an O(changes) solution in time or an O(living) solution in space. What we really want to do is (1) avoid doing any work at all on stable Quad4s; only spend processor time on the active ones, and (2) deallocate all-dead Quad4s, and (3) grow the set of active Quad4s when activity reaches the current borders.

We need more state bits, but fortunately we only need a small number; so small that I'm not even going to bit twiddle them. (The original Java implementation did, but it also used some of those bits for concerns such as optimizing the display logic.) Recall that we are tracking 32 regions of the 8 Quad3s in a Quad4 to determine if they are active, stable or dead. It should come as no surprise that we're going to do the same thing for a Quad4, and that once again we're going to maintain state for both the even and odd cycles:

enum Quad4State{ Active, Stable, Dead}

And then in Quad4:

public Quad4State State { get; set; } public Quad4State EvenState { get; set; }public Quad4State OddState { get; set; }public bool StayActiveNextStep { get; set; }

The idea here is:

• All Quad4s are at all times in exactly one of three buckets: active, stable and dead. Which bucket is represented by the State property.
• If a Quad4 is active then it is processed on each tick.
• If a Quad4 is stable then we draw it but do not process it on each tick.
• If a Quad4 is dead then we neither process nor draw it, and eventually we deallocate it. (We do not want to deallocate too aggressively in case it comes back to life in a few ticks.)

How then do we determine when an active Quad4 becomes stable or dead?

• If the stay active" flag is set, it stays active no matter what.
• The odd and even cycles each get a vote on whether an active Quad4 should become stable or dead.
• If both vote for dead, it becomes dead.
• If one votes for stable and the other votes for stable or dead, it becomes stable. (Exercise: under what circumstances is a Quad4 dead on the odd cycles but stable on the even?)
• If one or both vote for active, it stays active.

How do we determine if a stable (or dead but not yet deallocated) Quad4 becomes active? That's straightforward: if an active Quad4 has an active edge that abuts a stable Quad4, the stable one becomes active. Or, if there is no Quad4 there at all, we allocate a new one and make it active; this is how we achieve our goal of a dynamically growing board.

You might be wondering why we included a stay active" flag. There were lots of things about this algorithm that I found difficult to understand at first, but this took the longest for me to figure out, oddly enough.

This flag means there was activity on the edge of a neighbouring Quad4 recently". There are two things that could go wrong in that situation that we need to prevent. First, we could have an active Quad4 that is about to become stable or dead, but it has activity on a border that should cause it to remain active for processing. Second, we could have a stable (or dead) Quad4 that has just been marked as active because there is activity on a bordering Quad4, and we need to ensure that it stays active even though it wants to go back to being stable (or dead).

The easiest task to perform is to keep each Quad4 in one of three buckets. The original implementation did so by ensuring that every Quad4 was on exactly one of three double-linked lists, and I see no reason to change that. I have, however, encapsulated the linking and unlinking into a helper class:

interface IDoubleLink<T> where T : class{ T Prev { get; set; } T Next { get; set; }}sealed class DoubleLinkList<T> : IEnumerable<T> where T : class, IDoubleLink<T>{ public int Count { get; private set; } public void Add(T item) { ... } public void Remove(T item) { ... } public void Clear() { ... }}

I won't go through the implementation; it is more or less the standard double-linked list implementation you know from studying for boring technical interviews. The only unusual thing about it is that I've ensured that you can remove the current item from a list safely even while the list is being enumerated, because we will need to do that.

All the Quad4-level state manipulation will be done by our main class; we'll add some lists to it:

sealed class QuickLife : ILife, IReport{ private readonly DoubleLinkList<Quad4> active = new DoubleLinkList<Quad4>(); private readonly DoubleLinkList<Quad4> stable = new DoubleLinkList<Quad4>(); private readonly DoubleLinkList<Quad4> dead = new DoubleLinkList<Quad4>(); private Dictionary<(short, short), Quad4> quad4s; private int generation;

I'll skip the initialization code and whatnot.

We already have a method which allocates Quad4s and ensures their north/south, east/west, northwest/southeast references are initialized. We will need a few more helper functions to encapsulate some operations such as: make an existing Quad4 active, and if it does not exist, create it. Or, make an active Quad4 into a stable Quad4. They're for the most part just updating lists and state flags:

private Quad4 EnsureActive(Quad4 q, int x, int y){ if (q == null) return AllocateQuad4(x, y); MakeActive(q); return q;}private void MakeActive(Quad4 q){ q.StayActiveNextStep = true; if (q.State == Active) return; else if (q.State == Dead) dead.Remove(q); else stable.Remove(q); active.Add(q); q.State = Active;}private void MakeDead(Quad4 q){ Debug.Assert(q.State == Active); active.Remove(q); dead.Add(q); q.State = Dead;}private void MakeStable(Quad4 q){ Debug.Assert(q.State == Active); active.Remove(q); stable.Add(q); q.State = Stable;}

Nothing surprising there, except that as I mentioned before, when you force an already-active Quad4 to be active, it sets the stay active for at least one more tick" flag.

There is one more bit of list management mechanism we should consider before getting into the business logic: when and how do dead Quad4s get removed from the dead list and deallocated? The how is straightforward: run down the dead list, orphan all of the Quad4s by de-linking them from every living object, and the garbage collector will eventually get to them:

private void RemoveDead(){ foreach(Quad4 q in dead) { if (q.S != null) q.S.N = null; ... similarly for N, E, W, SE, NW quad4s.Remove((q.X, q.Y)); } dead.Clear();}

This orphans the entire dead list; the original implementation had a more sophisticated implementation where it would keep around the most recently dead on the assumption that they were the ones most likely to come back.

We have no reason to believe that this algorithm's performance is going to be gated on spending a lot of time deleting dead nodes, so we'll make an extremely simple policy; every 128 ticks we'll check to see if there are more than 100 Quad4s on the dead list.

private bool ShouldRemoveDead => (generation & 0x7f) == 0 && dead.Count > 100;public void Step(){ if (ShouldRemoveDead) RemoveDead(); if (IsOdd) StepOdd(); else StepEven(); generation += 1;}

All right, that's the mechanism stuff. By occasionally pruning away all-dead Quad4s we attain O(living) space usage. But how do we actually make this thing both fast and able to dynamically add new Quad4s on demand?

In keeping with the pattern of practice so far, we'll write all the code twice, once for the even cycle and once, slightly different, for the odd cycle. I'll only show the even cycle here.

Remember our original O(cells) prototype stepping algorithm:

private void StepEven(){ foreach (Quad4 q in quad4s) q.StepEven();}

We want to (1) make this into an O(changes) algorithm, (2) detect stable or dead Quad4s currently on the active list, and (3) expand the board by adding new Quad4s when the active region reaches the current edge. We also have (4) a small piece of bookkeeping from earlier to deal with:

private void StepEven(){ foreach (Quad4 q in active) // (1) O(changes) { if (!RemoveStableEvenQuad4(q)) // (2) remove and skip stable/dead { q.StepEven(); MakeOddNeighborsActive(q); // (3) expand } q.StayActiveNextStep = false; // (4) clear flag }}

The first one is straightforward; we now only loop over the not-stable, not-dead Quad4s, so this is O(changes), and moreover, remember that we consider a Quad4 to be stable if both its even and odd generations are stable, so we are effectively skipping all computations of Quad4s that contain only still Lifes and period-two oscillators, which is a huge win.

The fourth one is also straightforward: if the stay active for at least one step" flag was on, well, we made it through one step, so it can go off. If it was already off, it still is.

The interesting work comes in removing stable Quad4s, and expanding the board on the active edge. To do the former, we will need some more helpers that answer questions about the Quad4 and its neighbors; this is a method of Quad4:

public bool EvenQuad4OrNeighborsActive => EvenQuad4Active || (S != null && S.EvenNorthEdgeActive) || (E != null && E.EvenWestEdgeActive) || (SE != null && SE.EvenNorthwestCornerActive);

This is the Quad4 analogue of our earlier method that tells you if any of a 10*10 region is active; this one tells you if an 18*18 region is active, and for the same reason: because that region entirely surrounds the new shifted-to-the-southeast Quad4 we're computing. We also have the analogous methods to determine if that region is all stable or all dead; I'll omit showing them.

Let's look at our remove a stable/dead Quad4 from the active list" method. There is some slightly subtle stuff going on here. First, if the Quad4 definitely can be skipped for this generation because it is stable or dead, we return true. However, that does not guarantee that the Quad4 was removed from the active list! Second, remember that our strategy is to have both the even and odd cycles vote" on what should happen:

private bool RemoveStableEvenQuad4(Quad4 q){ if (q.EvenQuad4OrNeighborsActive) { q.EvenState = Active; q.OddState = Active; return false; }

If anything in the 18*18 region containing this Quad4 or its relevant neighbouring Quad4s are active, we need to stay active. We set the votes of both even and odd cycle back to active if they were different.

If nothing is active then it must be stable or dead. Is this 18*18 region dead? (Remember, we only mark it as dead if it is both dead and stable.)

 if (q.EvenQuad4AndNeighborsAreDead) { q.EvenState = Dead; q.SetOddQuad4AllRegionsDead(); if (!q.StayActiveNextStep && q.OddState == Dead) MakeDead(q); }

Let's go through each line here in the consequence of the if:

• Everything in an 18*18 region is dead and stable. The even cycle votes for death.
• We know that an 18*18 region is all dead and stable; that region entirely surrounds the odd Quad4. We therefore know that the odd Quad4 will be all dead on the next tick if it is not already, so we get aggressive and set all its region dead" bits now.
• If we're forcing this Quad4 to stay active then it stays active; however, even is still voting for death! We'll get another chance to kill this Quad4 on the next tick.
• By that same logic, if the odd cycle voted for death on the previous tick but the Quad4 stayed active for some reason then the odd cycle is still voting for death now. If that's true then both cycles are voting for death and the Quad4 gets put on the dead list.

We then have nearly identical logic for stability; the only difference is that if one cycle votes for stability, it suffices for the other cycle to vote for stability or death:

 else { q.EvenState = Stable; q.SetOddQuad4AllRegionsStable(); if (!q.StayActiveNextStep && q.OddState != Active) MakeStable(q); } return true;}

And finally: how do we expand into new space? That is super easy, barely an inconvenience. If we have just processed an active Quad4 on the even cycle then we've created a new odd Quad4 and in doing so we've set the activity bits for the 16 regions in the odd Quad4. If the south 16*2 edge of the odd Quad4 is active then the Quad4 to the south must be activated, and so on:

private void MakeOddNeighborsActive(Quad4 q){ if (q.OddSouthEdgeActive) EnsureActive(q.S, q.X, q.Y - 1); if (q.OddEastEdgeActive) EnsureActive(q.E, q.X + 1, q.Y); if (c.OddSoutheastCornerActive) EnsureActive(q.SE, q.X + 1, q.Y - 1); }

Once again we are taking advantage of the fact that the even and odd generations are offset by one cell; we only have to expand the board on two sides of each Quad4 during each tick, instead of all four. When we're completing an even cycle we check for expansion to the south and east for the upcoming odd cycle; when we're completing an odd cycle we check for expansion to the north and west for the upcoming even cycle.

It's a little hard to wrap your head around, but it all works. This staggered" property looked like it was going to be a pain when we first encountered it, but it is surprisingly useful; that insight is one of the really smart things about this algorithm.

There is a small amount of additional state management code I've got to put here and there but we've hit all the high points; see the source code for the exact changes if you are curious.

And that is that! Let's take it for a spin and run our usual 5000 generations of acorn".

Algorithm time(ms) size Mcells/s bits/cell O-timeNaive (Optimized): 4000 8 82 8/cell cellsAbrash (Original) 550 8 596 8/cell cellsStafford 180 8 1820 5/cell changeSparse array 4000 64 ? >128/living changeProto-QuickLife 1 770 8 426 4/cell cellsProto-QuickLife 2 160 8 2050 4/cell cellsQuickLife 65 20 ? 5/living* change

WOW!

We have an O(changes) in time and O(living) in space algorithm that maintains a sparse array of Quad4s that gives us a 20-quad to play with, AND it is almost three times faster than Stafford's algorithm on our benchmark!

Our memory usage is still pretty efficient; we are spending zero memory on all dead" Quad4s with all dead neighbours. We've added more state to each Quad4, so now for active and stable Quad4s we're spending around five bits per cell; same as Stafford's algorithm. (Though as I noted in my follow-up, he did find ways to get maintain a count of living neighbours" algorithms down to far fewer bits per cell.) I added an asterisk to the table above because of course an active or stable Quad4 will contain only 50% or fewer living cells, so this isn't quite right, but you get the idea.

Again, it is difficult to know how to characterize cells per second" for sparse array approaches where we have an enormous board that is mostly empty space that costs zero to process, so I've omitted that metric.

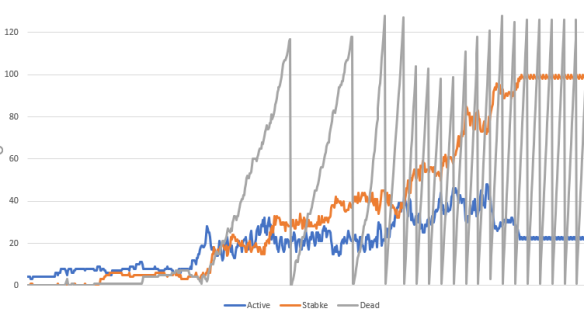
If you ran the code on your own machine you probably noticed that I added counters to the user interface to give live updates of the size of the active, stable and dead lists. Here's a graph of the first 6700 generations of acorn (click on the image for a larger version.)

You can really see how the pattern evolves from this peek into the workings of the algorithm!

• We start with a small number of active Quad4s; soon small regions of stability start to appear as the pattern spreads out and leaves still Lifes and period-two oscillators in its wake.
• The number of dead Quad4s remains very small right until the first glider escapes; from that moment on we have one or more gliders shooting off to infinity. In previous implementations they hit the wall of death, but now they are creating new active Quad4s in their bow shocks, and leaving dead Quad4s in their wakes.
• The stable count steadily grows as the active region is a smaller and smaller percentage of the total. Around the 5000th generation everything except the escaped gliders is stable, and we end up with around 100 stable Quad4s and 20 active Quad4s for the gliders.
• The action of our trivial little garbage collector" is apparent here; we throw away the trash only when there are at least 100 dead Quad4s in the list and we are on a generation divisible by 128, so it is unsurprising that we have a sawtooth that throws away a little over 100 dead Quad4s every 128 cycles.
• The blue line is proportional to time taken per cycle, because we only process active Quad4s.
• The sum of all three lines is proportional to total memory used.

That finishes off our deep dive into Alan Hensel's QuickLife algorithm. I was quite intimidated by this algorithm when I first read the source code, but once you name every operation and reorganize the code into functional areas it all becomes quite clear. I'm glad I dug into it and I learned a lot.

Coming up on FAIC:

We've seen a lot of varied ways to solve the problem of simulating Life, and there are a pile more in my file folder of old articles from computer magazines that we're not going to get to in this series. Having done this exploration into many of them and skimmed a lot more, two things come to mind.

First, so far they all feel kind of the same to me. There is some sort of regular array of data, and though I might layer object-oriented features on top of it to make the logic easier to follow or better encapsulated, fundamentally we're doing procedural work here. We can be more or less smart about what work we can avoid or precompute, and thereby eliminate or move around the costs, but the ideas are more or less the same.

Second, every optimization we've done increases the amount of redundancy, mutability, bit-twiddliness, and general difficulty of understanding the algorithm.

Gosper's algorithm stands in marked contrast.

• There is no array of cells" at all
• The attack on the problem is purely functional programming; there is very little state mutation.
• There is no redundancy. In the Abrash, Stafford and Hensel algorithms we had ever-increasing amounts of redundant state that had to be carefully kept in sync with the board state. In Gosper's algorithm, there is board state and nothing else.
• No attempt whatsoever is made to make individual cells smaller in memory, but it can represent grids a trillion cells on a side with a reasonable amount of memory.
• It can compute trillions of ticks per second on quadrillion-cell grids on machines that only do billions of operations per second.
• Though there are plenty of tricky details to consider in the actual implementation, the core algorithm is utterly simple and elegant. The gear that does the optimization of the algorithm uses off-the-shelf parts and completely standard, familiar functional programming techniques. There is no mucking around with fiddly region change tracking, or change lists, or bit sets, or any of those mechanisms.
• And extra bonus, the algorithm makes zoom in or out arbitrarily far" in the UI super easy, which is nice for large boards.

This all sounds impossible. It is not an exaggeration to say that learning about this algorithm changed the way I think about the power of functional programming and data abstraction, and I've been meaning to write a blog about it for literally over a decade.

It will take us several episodes to get through it:

• Next time on FAIC we'll look at the core data structure. We'll see how we can compress large boards down to a small amount of space.
• Then we'll closely examine the update the UI" algorithm and see how we can get a nice new feature.
• After that we'll build the step forward one generation algorithm" and do some experiments with it.
• Finally, we'll discover the key insight that makes Gosper's algorithm work: you can enormously compress time if you make an extremely modest addition of extra space.
• We will finish off this series with an answer to a question I've been posing for some time now: are there patterns that grow quadratically?