Life, part 32

All right, after that excessively long introduction let's get into Gosper's algorithm, also known as HashLife" for reasons that will become clear quite soon. Since the early days of this series I've mostly glossed over the code that does stuff like changing individual cells in order to load in a pattern, or the code that draws the UI, but Gosper's algorithm is sufficiently different that I'm going to dig into every part of the implementation.

The first key point to understand about Gosper's algorithm is that it only has one data structure. One way to describe it is:

A quad is an immutable complete tree where every non-leaf node has exactly four children which we call NE, NW, SE, SW, and every leaf is either alive or dead.

However the way I prefer to describe it is via a recursive definition:

• A 0-quad is either alive or dead.
• An n-quad for n > 0 is four (n-1) quads.

Let's write the code!

sealed class Quad{ public const int MaxLevel = 60;

Because there will be math to do on the width of the quad and I want to keep doing the math in longs instead of BigIntegers, I'm going to limit us to a 60-quad, max. Just because it is a nice round number less than the 64 bits we have in a long.

Now, I know what you're thinking. Eric, if we built a monitor with a reasonable pixel density to display an entire 60-quad it would not fit inside the orbit of Pluto and it would have more mass than the sun." A 60-quad is big enough for most purposes. I feel good about this choice. However I want to be clear that in principle nothing is stopping us from doing math in a larger type and making arbitrarily large quads.

Here are our two 0-quads:

public static readonly Quad Dead = new Quad();public static readonly Quad Alive = new Quad();

And for the non-0-quads, the child (n-1) quads:

public Quad NW { get; }public Quad NE { get; }public Quad SE { get; }public Quad SW { get; }

We will need to access the level and width of a quad a lot, so I'm going to include the level in every quad. The width we can calculate on demand.

public int Level { get; }public long Width => 1L << Level;

We'll need some constructors. There's never a need to construct 0-quads because we have both of them already available as statics. For reasons which will become apparent later, we have a public static factory for the rest.

public static Quad Make(Quad nw, Quad ne, Quad se, Quad sw){ Debug.Assert(nw.Level == ne.Level); Debug.Assert(ne.Level == se.Level); Debug.Assert(se.Level == sw.Level); return new Quad(nw, ne, se, sw);}private Quad() => Level = 0;private Quad(Quad nw, Quad ne, Quad se, Quad sw){ NW = nw; NE = ne; SE = se; SW = sw; Level = nw.Level + 1;}

We're going to need to add a bunch more stuff here, but this is the basics.

Again I know what you're probably thinking: this is bonkers. In QuickLife, a 3-quad was an eight byte value type. In my astonishingly wasteful implementation so far, a single 0-quad is a reference type, so it is already eight bytes for the reference, and then it contains four more eight byte references and a four byte integer that is never more than 60. How is this ever going to work?

Through the power of persistence, that's how. As I've discussed many times before on this blog, a persistent data structure is an immutable data structure where, because every part of it is immutable, you can safely re-use portions of it as you see fit. You therefore save on space.

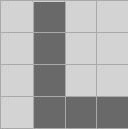
Let's look at an example. How could we represent this 2-quad?

Remember, we only have two 0-quads and we cannot make any more. The naive way would be to make this tree:

But because every one of these objects is immutable, we could instead make this tree, which has one fewer object allocation:

This is the second key insight to understanding how Gosper's algorithm works: it uses a relatively enormous data structure for each cell, but it achieves compression through deduplication:

• There are only two possible 0-quads, and we always re-use them.
• There are 16 possible 1-quads. We could just make 16 objects and re-use them.
• There are 65536 possible 2-quads, but the vast majority of them we never see in a given Life grid. The ones we do see, we often see over and over again. We could just make the ones we do see, and re-use them.

The same goes for 3-quads and 4-quads and so on. There are exponentially more possibilities, and we see a smaller and smaller fraction of them in any board. Let's memoize the Make function!

We're going to make heavy use of memoization in this algorithm and it will have performance implications later, so I'm going to make a relatively fully-featured memoizer whose behaviour can be analyzed:

sealed class Memoizer<A, R>{ private Dictionary<A, R> dict; private Dictionary<A, int> hits; private readonly Func<A, R> f; [Conditional("MEMOIZER_STATS")] private void RecordHit(A a) { if (hits == null) hits = new Dictionary<A, int>(); if (hits.TryGetValue(a, out int c)) hits[a] = c + 1; else hits.Add(a, 1); } public R MemoizedFunc(A a) { RecordHit(a); if (!dict.TryGetValue(a, out R r)) { r = f(a); dict.Add(a, r); } return r; } public Memoizer(Func<A, R> f) { this.dict = new Dictionary<A, R>(); this.f = f; } public void Clear(Dictionary<A, R> newDict = null) { dict = newDict ?? new Dictionary<A, R>(); hits = null; } public int Count => dict.Count; public string Report() => hits == null ? "" : string.Join("\n", from v in hits.Values group v by v into g select $"{g.Key},{g.Count()}");}

The core logic of the memoizer is the same thing I've presented many times on this blog over the years: when you get a call, check to see if you've memoized the result; if you have not, call the original function and memoize the result, otherwise just return the result.

I've added a conditionally-compiled hit counter and a performance report that tells me how many items were hit how many times; that will give us some idea of the load that is being put on the memoizer, and we can then tune it.

Later in this series we're going to need to reset" a memoizer and optionally we'll need to provided pre-memoized" state, so I've added a Clear" method that optionally takes a new dictionary to use.

The memoizer for the Make" method can be static, global state so I'm going to make a helper class for the cache. (I did not need to; this could have been a static field of Quad. It was just convenient for me while I was developing the algorithm to put the memoizers in one central location.)

static class CacheManager{ public static Memoizer<(Quad, Quad, Quad, Quad), Quad> MakeQuadMemoizer { get; set; }}

We'll initialize it when we create our first Quad:

static Quad(){ CacheManager.MakeQuadMemoizer = new Memoizer<(Quad, Quad, Quad, Quad), Quad>(UnmemoizedMake);}

And we'll redo the Make static factory:

private static Quad UnmemoizedMake((Quad nw, Quad ne, Quad se, Quad sw) args){ Debug.Assert(args.nw.Level == args.ne.Level); Debug.Assert(args.ne.Level == args.se.Level); Debug.Assert(args.se.Level == args.sw.Level); return new Quad(args.nw, args.ne, args.se, args.sw);}public static Quad Make(Quad nw, Quad ne, Quad se, Quad sw) => CacheManager.MakeQuadMemoizer.MemoizedFunc((nw, ne, se, sw));

All right, we have memoized construction of arbitrarily large quads. A nice consequence of this fact is that all quads can be compared for equality by reference equality. In particular, we are going to do two things a lot:

• Create an arbitrarily large empty quad
• Ask is this arbitrarily large quad an empty quad"?

We're on a memoization roll here, so let's keep that going and add a couple more methods to Quad, and another memoizer to the cache manager (not shown; you get how it goes.)

private static Quad UnmemoizedEmpty(int level){ Debug.Assert(level >= 0); if (level == 0) return Dead; var q = Empty(level - 1); return Make(q, q, q, q);}public static Quad Empty(int level) => CacheManager.EmptyMemoizer.MemoizedFunc(level);public bool IsEmpty => this == Empty(this.Level);

The unmemoized construct an empty quad" function can be as inefficient as we like; it will only be called once per level. And now we can quickly tell if a quad is empty or not. Well, relatively quickly; we have to do a dictionary lookup and then a reference comparison.

What then is the size in memory of an empty 60-quad? It's just 61 objects! The empty 1-quad refers to Dead four times, the empty 2-quad refers to the empty 1-quad four times, and so on.

Suppose we made a 3-quad with a single glider in the center; that's a tiny handful of objects. If you then wanted to make a 53-quad completely filled with those, that only increases the number of objects by 50. Deduplication is super cheap with this data structure - provided that the duplicates are aligned on boundaries that are a power of two of course.

A major theme of this series is: find the characteristics of your problem that admit to optimization and take advantage of those in pursuit of asymptotic efficiency; don't worry about the small stuff. Gosper's algorithm is a clear embodiment of that principle. We've got a space-inefficient data structure, we're doing possibly expensive dictionary lookups all over the show; but plainly we can compress down grids where portions frequently reoccur into a relatively small amount of memory at relatively low cost.

Next time on FAIC: There are lots more asymptotic wins to come, but before we get into those I want to explore some mundane concerns:

• If portions of the data structure are reused arbitrarily often then no portion of it can have a specific location. How are we going to find anything by its coordinates?
• If the data structure is immutable, how do we set a dead cell to alive, if, say, we're loading in a pattern?
• How does the screen drawing algorithm work? Can we take advantage of the simplicity of this data structure to enable better zooming in the UI?