Asymptotic series for gamma function ratios
Applications of statistics often require working with
for large x and fixed and .
The simplest approximation to this ratio of gamma functions is
You can do a little better [1] with
where c = ( + - 1)/2.
To get more accuracy we'll need more terms. Tricomi and Erdelyi worked out the full asymptotic series 70 years ago:
Here Bn is the generalized Bernoulli polynomial," a.k.a. the Norlund polynomial [3].
There's no simple way to state the coefficients in the series above. The expression in terms of Norlund polynomials is compact, but then the Norlund polynomials are a bit complicated to define. The can be calculated in Mathematica with NorlundB, and so the coefficients would be
Binomial[-, n] NorlundB[n, -+1, ]
in Mathematica.
Let's see how the various approximations compare in an example.
{, } = {3.4, 5.6} f[x_] := Gamma[x+]/Gamma[x+] f1[x_] = x^(-) f2[x_] = (x + (+-1)/2)^(-) f3[x_] = Sum[Binomial[-, n] NorlundB[n, -+1, ] x^{--n}, {n, 0, 2}]We can plot the exact function f and its approximations with
LogPlot[{f[x], f1[x], f2[x], f3[x]}, {x, 10, 15}, PlotLabels -> Automatic]This gives the following.
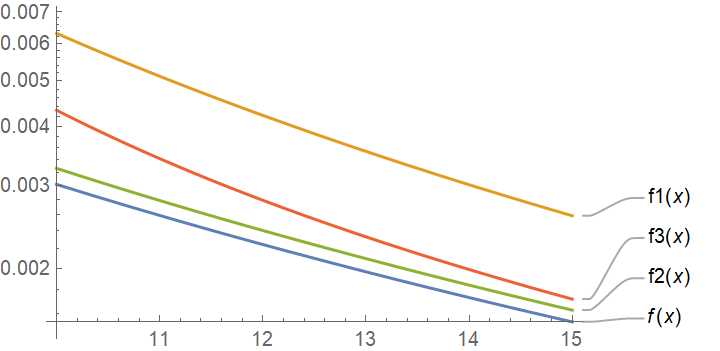
It's interesting that the approximation f2 works really well and is the most accurate approximation over the range shown. For large enough x, say x = 1000, the series approximation f3 will be more accurate.
***
[1] A. Laforgia, P. Natalini. On the asymptotic expansion of a ratio of gamma functions. Journal of Mathematical Analysis and Applications. Volume 389, Issue 2, 15 May 2012, pp. 833-837.
[2] F. G. Tricomi, A. Erdelyi. The asymptotic expansion of a ratio of gamma functions. Pacific J. Math. 1 (1951), pp. 133-142.
[3] The authors in [1] quote this formula from [2] but leave out the binomial coefficient. Note that the binomial coefficient parameters are not necessarily positive integers and so the binomial coefficients should be interpreted in the sense of the most general definition.
The post Asymptotic series for gamma function ratios first appeared on John D. Cook.