A stiffening spring
Imagine a spring with stiffness k1 attached to a ceiling and a mass m1 handing from the spring.
There's a second spring attached to the first mass with stiffness k2 and a mass m2 handing from that.
The motion of the system is described by the pair of differential equations
If the second spring were infinitely stiff, the two masses would be joined with a rigid rod, and so the system would act like a single mass m1 + m2 hanging from the first spring. This motion would be described by the single differential equation
So it's not surprising that as k2 gets stiffer, the solution to the two-mass system converges to the solution to the system with a single combined mass. This is proven in [1].
However, what is missing from [1] is any visualization of how the solution to the two-mass system converges to that of the combined-mass system.
The plot below shows solutions for k2 equal to 10, 100, and 1000, and finally the system to the combined-mass system, labeled k2 = . I used k1 = 1, m1 = 3, and m2 = 5.
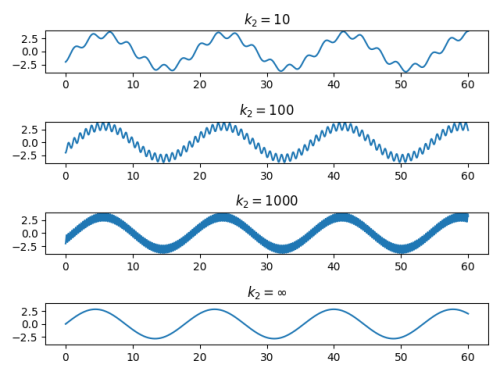
The coupled-mass system has a high-frequency component due to the oscillation of the second mass relative to the first one.
The authors in [1] show that the amplitude of the high-frequency component decays as k2 goes to infinity, though this is not apparent from the plots above. This is due to a limitation of the numerical method used to produce the plots.
Analytical solutionThe numerical solution above raises two questions. First, how fast should the amplitude of high frequency component decay. Second, why did the numerical method apparently get the frequency of this component correct but the amplitude wrong?
The second question is more difficult and will have to wait for another post. The first question, however, we can settle fairly quickly.
The authors in [1] make the simplifying assumption that the two masses are equal to 1. They then define show that
where the ds are constants that depend on initial conditions but not on the spring stiffnesses. and
4, the frequency of the low frequency component, approaches a finite limit as k2 ,
2, the frequency of the high frequency component, is approximately (2k2) for large k2.
The amplitude of the high frequency component should be inversely proportional to its frequency.
More differential equation posts[1] K. E. Clark and S. Hill. The Effects of a Stiffening Spring. The College Mathematics Journal , Nov., 1999, Vol. 30, No. 5 (Nov., 1999), pp. 379-382
The post A stiffening spring first appeared on John D. Cook.