Simple approximation for perimeter of an ellipse
The perimeter of an ellipse cannot be computed in closed form. That is, no finite combination of elementary functions will give you the exact value. But we will present a simple approximation that is remarkably accurate.
So this post has two parts: exact calculation, and simple approximation.
Exact perimeterThe perimeter can be computed exactly in terms of an elliptic integral. The name's not a coincidence: elliptic integrals are so named because they were motivated by trying to find the perimeter of an ellipse.
Let a be the length of the major semi-axis and b the length of the minor semi-major axis. So a > b, and if our ellipse is actually a circle, a = b = r.
If is the eccentricity of our ellipse,
^2 = 1 - b^2 / a^2
and the perimeter is give by
p = 4a E(^2)
where E is the complete elliptic integral of the second kind." This function has popped up several times on this blog, most recently in the post about why serpentine walls save bricks.
You could calculate the perimeter of an ellipse in Python as follows.
from scipy.special import ellipe def perimeter(a, b): assert(a > b > 0) return 4*a*ellipe(1 - (b/a)**2)Simple approximation
But what if you don't have a scientific library like SciPy at hand? Is there a simple approximation to the perimeter?
In fact there is. In [1] the authors present the approximation
If we define the effective radius as r = p/2, then the approximation above says
in the notation of Hardy, Littlewood, and Polya, where x = (a, b).
We could code this up in Python as follows.
def rmean(r, x): n = len(x) return (sum(t**r for t in x)/n)**(1/r) def approx(a, b): return 2*pi*rmean(1.5, (a, b))
It would have been less code to write up approx directly without defining rmean, but we'll use rmean again in the next post.
For eccentricity less than 0.05, the error is less than 10-15, i.e. the approximation is correct to all the precision in a double precision floating point number. Even for fairly large eccentricity, the approximation is remarkably good.
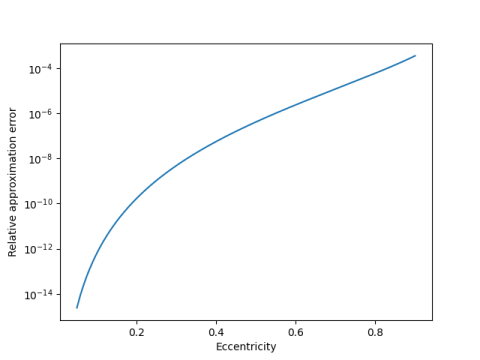
The eccentricity of Pluto's orbit is approximately 0.25. So the approximation above could compute the perimeter of Pluto's orbit to nine significant figures, if the orbit were exactly an ellipse. A bigger source of error would be the failure of the orbit to be perfectly elliptical.
If an ellipse has major axes several times longer than its minor axis, the approximation here is less accurate, but still perhaps good enough, depending on the use. There is an approximation due to Ramanujan that works well even for much more eccentric ellipses, though it's a little more complicated.
To my mind, the most interesting thing here is the connection to r-norms. I'll explore that more in the next post, applying r-norms to the surface area of an ellipsoid.
[1] Carl E. Linderholm and Arthur C. Segal. An Overlooked Series for the Elliptic Perimeter. Mathematics Magazine, June 1995, pp. 216-220
The post Simple approximation for perimeter of an ellipse first appeared on John D. Cook.