Real radical roots
The previous post Does chaos imply period 3? ended with looking at a couple cubic polynomials whose roots have period 3 under the mapping f(x) = 4x(1-x). These are
64 x^3 - 112 x^2 + 56 x - 7
and
64 x^3 - 96 x^2 + 36 x - 3.
I ended the post by saying you could find their roots numerically using the NSolve function in Mathematica.
What if you wanted to find the roots exactly? You could try using the NSolve function rather than the NSolve solve function, but you won't get anything back. Doesn't Mathematica know how to solve a cubic equation? Yes it does, and you can force it to use the cubic equation by using the ToRadicals function.
If you apply ToRadicals to the roots, Mathematica will give you the roots in radical form, with expressions involving complex numbers. For example, here's the smallest root of the first polynomial:
But the roots of these polynomials are clearly real as you can see from their graphs.
.
If we didn't have access to a graph, we could show that the roots are real and distinct by computing the discriminant and seeing that it is positive.
Casus irreducibilisThe polynomials have degree less than 5, so their roots can be expressed in terms of radicals. And the roots are real. But they cannot be expressed in terms of real radicals!
This an example of the casus irreducibilis." Most cubic equations with real roots cannot be solved using real radicals. The casus irreducibilis theorem says that the roots of a cubic polynomial can be written in terms of real radicals if and only if one of the roots is rational.
This says there's a sort of excluded middle ground: the roots cannot involve cubic roots with real numbers. They are either simpler or more complex. If there is a rational root, you can factor it out and find the other two roots with the quadratic equation, i.e. only using square roots, not cubic roots. But if there is no rational root, expressing the roots in terms of radicals requires cube roots and complex numbers.
Our polynomialsThe rational root test says that if a polynomial has a rational root p/q then q must be a factor of the leading coefficient and p must be a factor of the constant term. So in our first cubic
64 x^3 - 112 x^2 + 56 x - 7
any rational root must have denominator 1, 2, 4, ..., 64 and numerator either 1 or 7. We can check all the possibilities and see that none of them are zeros.
Similarly the only possible rational roots of
64 x^3 - 96 x^2 + 36 x - 3
must have denominator 1, 2, 4, ..., 64 and numerator either 1 or 3, and none of them are zeros.
So the roots of our cubic polynomials can be expressed in terms of radicals, but not without complex numbers, even though the roots are all real.
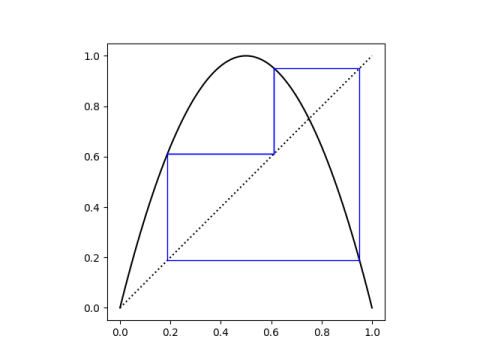
Unstable orbitThe reason we were interested in these two polynomials is that we were looking for orbits of period 3 under iterations of 4x(1-x). And we found them. But they form an unstable orbit.
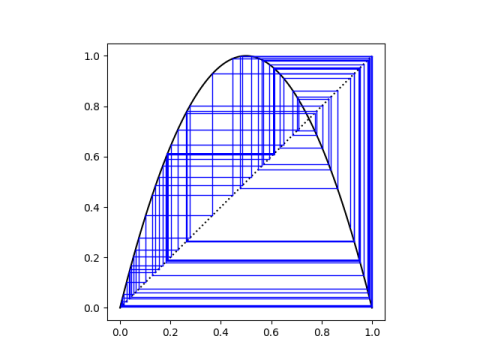
If we make a cobweb plot of the iterations starting at any one of the roots, it appears that multiple applications of 4x(1-x) just rotate between the three roots.
But with a few more iterations-the plot below shows 100 iterations-we can see that these points are not stable. Unless you start exactly on one of the roots, which you cannot since they're irrational, you will wander away from them.