Self-reproducing cellular automata

Edward Fredkin is best known these days for the Fredkin gate, a universal reversible circuit.

I recently found out that Fredkin was one of the pioneers in cellular automata. His student Edwin Banks describes a cellular automaton introduced by Fredkin [1].

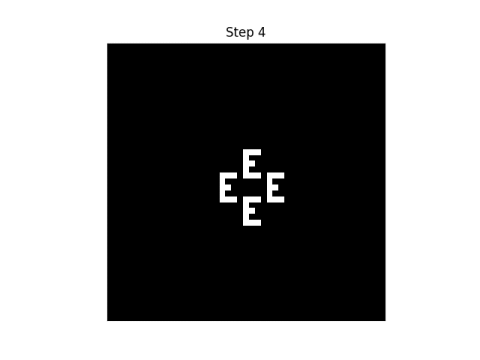
Edward Fredkin of MIT has described the following interesting cellular space. If the states are 0 and 1 and if the result state is obtained by taking the sum of the neighbors, modulo 2, then every initial configuration will reproduce copies of itself about the initial configuration.

In other words, start with some bit pattern in an infinite checkerboard of bits. Then at each step, replace each bit by the parity of the sum of the neighboring bits. Eventually you'll see copies of that original pattern.

There's some ambiguity regarding what neighbors" means. Banks' dissertation considers the neighbors of a bit to be the bits to the north, south, east, and west, and this implies that Banks has these neighbors in mind when he describes Fredkin's automaton. Other sources say Fredkin also considered diagonally adjacent bits as part of the neighborhood, i.e. northwest, northeast, southwest, and southeast.

Banks goes on to say

Terry Winograd (1970) generalized this result showing that any neighborhood, not just the four nearest neighbors, and any number of dimensions still yields the same results.

I take it by the four nearest neighbors" the neighbors to the north, south, east, and west. I'm not sure what the any neighborhood" means in Winograd's theorem; I imagine there must be some implied restriction.

In any case, I'll show by example that both definitions of neighborhood" discussed above lead to reproducing the original pattern, though they do not reproduce it in the same way.

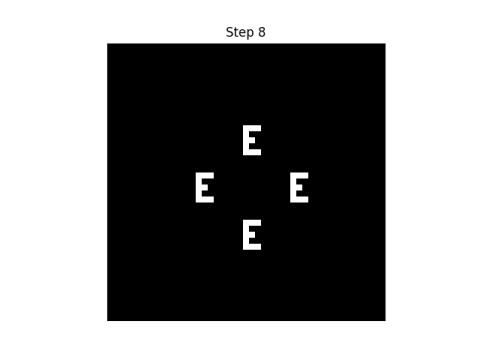
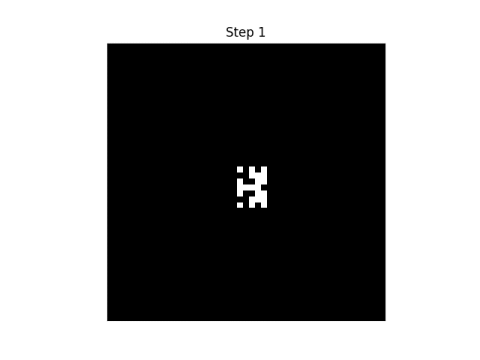
I'll start with an E' in the middle of a grid. The black squares represent 0s and the white squares represent 1s.

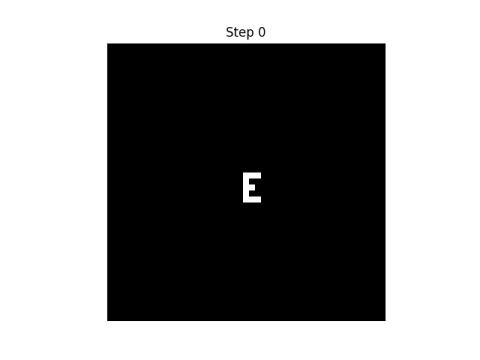
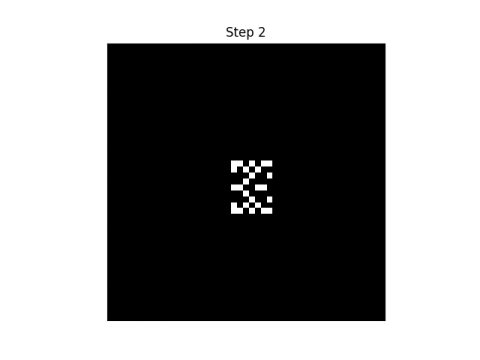
Here are the first eight steps in evolving this pattern, using the rule that neighbor" only includes north, south, east, and west neighbors.

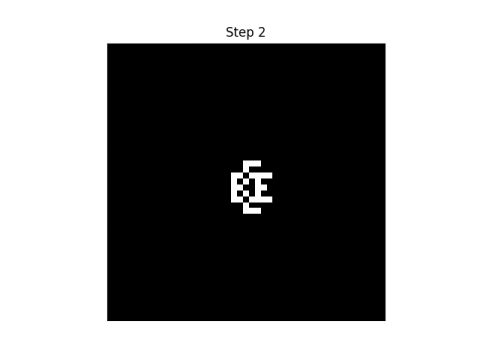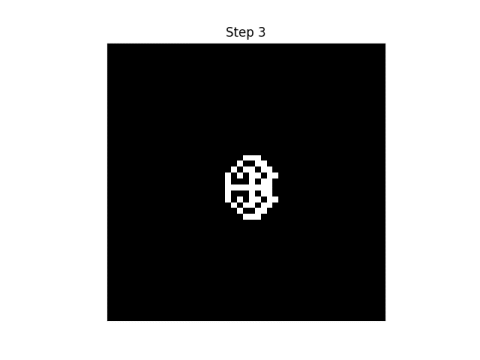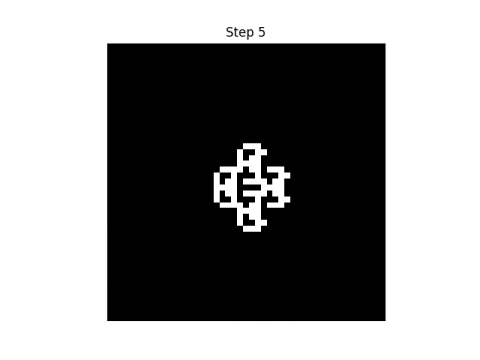If we consider each point to have eight neighbors, i.e. we include diagonals, here's what the first eight steps look like.

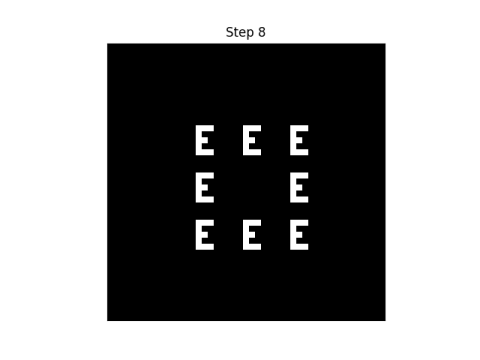Update: Here's an animated version of the first automaton

and the second

See the next post for a generalization using more than two states per cell, using colors rather than black and white cells. If the number of colors is prime, and you take the sum of the neighboring states mod p rather than mod 2, you get analogous results.

[1] Edwin R. Banks, Information Processing and Transmission in Cellular Automata. MIT dissertation. January 1971.

The post Self-reproducing cellular automata first appeared on John D. Cook.