HAKMEM, AGM, and Pi
HAKMEM is a collection of tricks and trivia from the MIT AI lab written in 1972. I've mentioned HAKMEM here before. The image below came from HAKMEM item 123, explained here.
I ran across HAKMEM item 143 while writing my previous two blog posts about the arithmetic-geometric mean (AGM). This entry, due to Gene Salamin, says that
for large n. In fact, n doesn't have to be very large. The expression on the right converges exponentially as n grows.
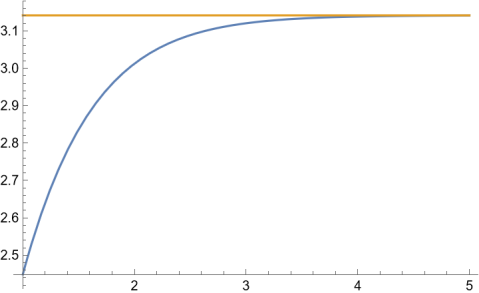
Here's the Mathematica code that produced the plot above.
Plot[{2 n ArithmeticGeometricMean[1, 4 Exp[-n]], Pi}, {n, 1, 5}, PlotRange -> All]If you have e to a large number of decimals, you could compute efficiently by letting n be a power of 2, computing e-n by repeatedly squaring 1/e, and using the AGM. Computing the AGM is simple. In Python notation, iterate
a, b = (a+b)/2, sqrt(a*b)
until a and b are equal modulo your tolerance.
The post HAKMEM, AGM, and Pi first appeared on John D. Cook.