Mentally compute cosine
Ronald Doerfler presents a simple approximation for the cosine of an angle in degrees in his book Dead Reckoning.
cos d 1 - d(d + 1)/7000
The approximation is good to about three digits for angles between 0 and 40.
Although cosine is an even function, the approximation above is not, and the error is larger for negative angles. But there's no need to use negative values since cos(-d) = cos(d). Just compute the cosine of the absolute value of the angle.
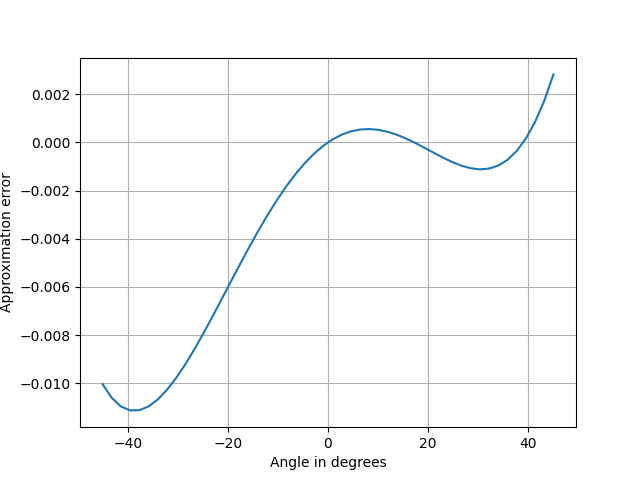
The simplest thing to do would have been to use a Taylor approximation, but Taylor approximations don't work well over a large interval; they're excessively accurate near the middle and not accurate enough at the ends. The error at 40 would have been 100x larger. Also, the Taylor approach would have required multiplying or dividing by a more mentally demanding number than 7000.
If we wanted to come up with a quadratic approximation for a computer rather than for a human, we could squeeze out more accuracy. The error curve over the interval [0, 40] dips down significantly more than it goes up. An optimal approximation would go up and down about the same amount.
Related postsThe post Mentally compute cosine first appeared on John D. Cook.