FM signal approximation
FM radio transmits a signal by perturbing (modulating) the frequency of a carrier wave. If the carrier has frequency and the signal has frequency q, then the FM signal is
cos(t + cos(qt)).
To understand the modulated signal, it's useful to write it as a sum of simple sines and cosines with no modulation. I wrote about how to do this exactly using Bessel functions. Today I'll write about an approximation that's easier to understand and work with, assuming the modulation index is small.
Here's the approximation:
cos(t + cos(qt)) cos t + ( sin ( + q)t + sin ( - q)t ).
This says that to a good approximation, the modulation term adds two sine waves to the carrier, one that adds the signal frequency to the carrier frequency and one that subtracts it.
To establish the approximation and see how the error depends on , subtract the right side from the left and expand as a Taylor series in . The first non-zero term in the series is
- cos(qt)^2 cos(t) ^2
and so if is small, the approximation error is very small. For example, if = 0.1, then the approximation error is on the order of 0.005.
As an example, let = 10, q = 2, and = 0.1. Then
cos(10t + 0.1 cos 2t) cos 10t + 0.05 ( sin 12t + sin 8t )
and the approximation error is plotted below.
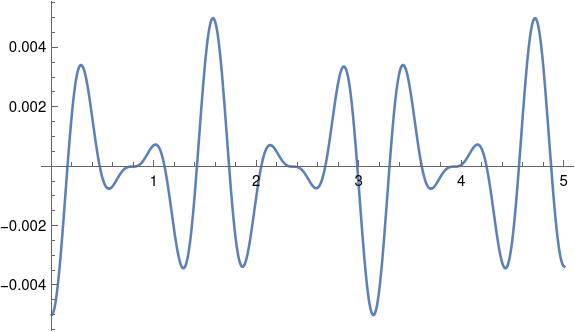
As predicted, the amplitude of the error is around 0.005, while the amplitude of the FM signal is 1.
The post FM signal approximation first appeared on John D. Cook.