Much ado about NaN

I ran across a GitHub repo today that features an amusing hack using the sign bit of NaNs for unintended purposes. This is an example of how IEEE floating point numbers have a lot of leftover space devoted to NaNs and infinities. However, relative to the enormous number of valid 64-bit floating point numbers, this waste is negligible.

But when you scale down to low-precision floating point numbers, the overhead of the strange corners of IEEE floating point becomes significant. Interest in low-precision floating point comes from wanting to pack more numbers into memory at the same time when you don't need much precision. Floating point numbers have long come in 64 bit and 32 bit varieties, but now there are 16 bit and even 8 bit versions.

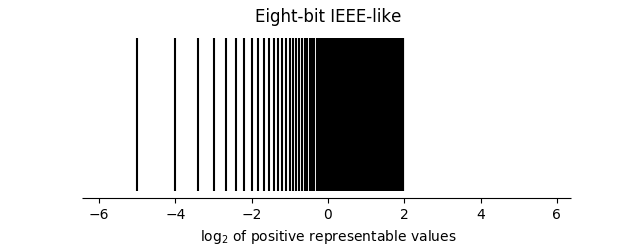
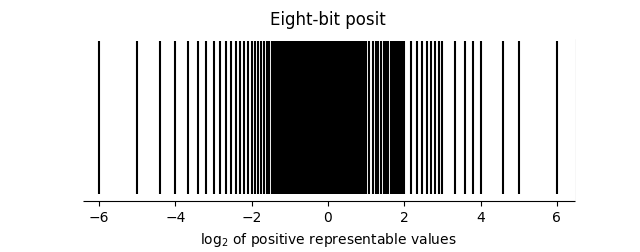
There are advantages to using completely new floating point formats for low precision numbers rather than scaling down the venerable IEEE format. Posit numbers have only one special number, a point at infinity. Every other bit pattern corresponds to a real number. Posits are also more usefully distributed, as illustrated in the image below, taken from here.

IEEE float posts

• Anatomy of a floating point number
• Floating point exceptions
• Two kinds of zeros

Posit number posts

• Anatomy of a posit number
• One infinity or two?
• Comparing IEEE and posit range

The post Much ado about NaN first appeared on John D. Cook.