Sawtooth and replicative functions
Here's something I ran across in Volume 2 of Donald Knuth's The Art of Computer Programming.
Knuth defines the sawtooth function by
((x)) = x - (x + x)/2.
Here's a plot.
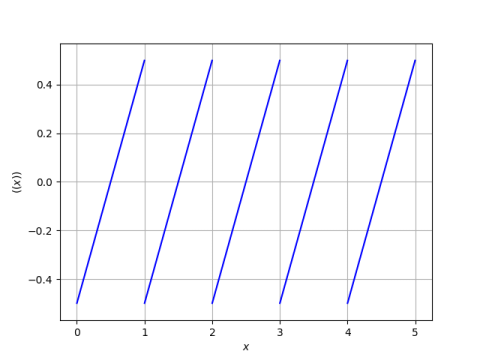
This is an interesting way to write the sawtooth function, one that could make it easier to prove things about, such as the following theorem. For positive integers n, we have
It's not at all obvious, at least to me, that this should be true.
Knuth does not give a proof but leaves the proof to Exercise 2 in Section 3.3.3. I suppose you could prove it by slugging it out with floor and ceiling identities, but I looked at the solutions to see whether Knuth has a more elegant proof.
The solution for Exercise 2 says to see exercises 38 and 39 in Volume 1, section 1.2.4. These exercises break the problem of proving the theorem above into smaller parts. They also generalize the problem, defining a function f to be replicative if it satisfies the equation
The theorem above says that the sawtooth function is replicative. Other examples of replicative functions include the floor function and the function that takes x to x - .
Related postsThe post Sawtooth and replicative functions first appeared on John D. Cook.