Triangles on a pseudosphere
The previous post was about triangles on a sphere. This post will be about triangles on a pseudosphere.
A pseudosphere looks something like the bell of a trumpet or a trombone.
Here's a plot of a pseudosphere.
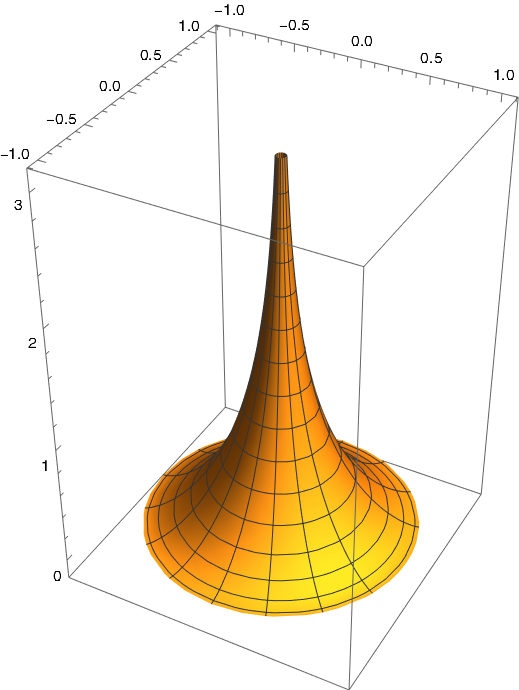
This was created in Mathematica with the code
ParametricPlot3D[ { Cos[p] Sech[t], -Sin[p] Sech[t], t - Tanh[t] }, {t, 0, 4}, {p, 0, 2 Pi} ]The pseudosphere has constant negative curvature just as the sphere has constant positive curvature.
By curvature I mean specifically Gaussian curvature, the product of the sectional curvature in orthogonal directions at each point. A sphere curves the same way in all directions. A pseudosphere curves opposite ways in different directions. Coordinate lines through a point are convex in one direction and concave in another. Their sectional curvatures have opposite signs and so their product is negative.
A spherical triangle is formed by great circles connecting the vertices of the triangles. Great circles are the geodesics on a sphere.
A pseudospherical triangle is a triangle formed by geodesics on the pseudosphere. These are the straight" lines in the hyperbolic geometry of the surface.
On a sphere, the interior angles of a triangle add up to more than , and in fact the amount by which the sum of the angles exceeds is proportional to the area of the triangle.
On a pseudosphere, the interior angles of a triangle add up to less than . And just as in the case of the sphere, the difference between the sum of the angles and , now negative, is proportional to the area. This result was discovered by Johann Heinrich Lambert (1728-1777).
On a sphere or a pseudosphere, the interior angles of a small triangle add up to nearly . As triangles get larger, the sum increases on a sphere but decreases on a pseudosphere.
The general principle behind both of these cases is the local Gauss-Bonnet theorem. For any surface, let T be triangle whose sides are geodesics. Then the integral of the Gaussian curvature over T is equal to the sum of the interior angles of T minus .
When a surface has constant curvature, the integral of curvature over a region is proportional to the area of the region. So on a sphere or pseudosphere, the area of a geodesic triangle is proportional to the sum of the interior angles minus .
The local Gauss-Bonnet theorem holds when the sides of a triangle are not geodesics, but in that case the theorem has an extra term, the integral of the geodesic curvature along the sides. Since the geodesic curvature of a geodesic is zero, this term drops out for geodesic triangles.
Related postsThe post Triangles on a pseudosphere first appeared on John D. Cook.