Four, five, and nine lemmas
This post is similar in spirit to the previous post: reducing mathematical theorems to moves in a board game by looking at things from a ridiculously high level.
The theorems we'll be looking at are known as the four lemma, the five lemma, and the nine lemma. The nine lemma is also known as the 3*3 lemma.
All the lemmas start with a commutative diagram. A diagram is commutative if any two ways of getting from one place to another are equal. If the arrows represent functions, then the diagram implies certain compositions of functions are equal.
Given hypotheses about most of the arrows in a diagram, the theorems conclude something about the rest of the arrows. This general category of theorems is known as diagram chasing. The proofs are tedious but shallow. If a theorem in topology, for example, were formulated as a diagram chase, someone with no intuition for topology could prove the theorem by applying the rules of a simple game.
The meaning of the dots and arrows isn't important for this post, but you could think of the dots in the diagram as groups and the arrows as homomorphisms between groups. More generally you could think of the dots as objects in an Abelian category and the arrows as morphisms between objects.
The four lemmaThe four lemma starts with with a commutative diagram of the following shape.
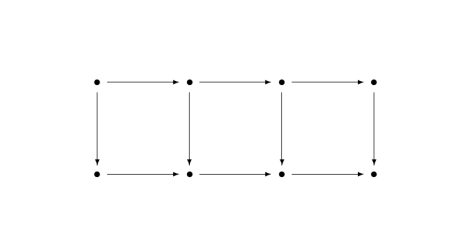
It's called the four lemma because there are four dots across each row.
There are two versions of the four lemma. Both make assumptions about the rows and three out of the four columns and conclude something about the fourth column.
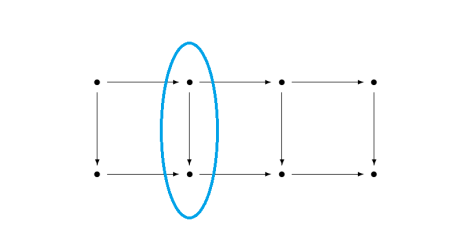
In the first part of the lemma, we have hypotheses about the two rows, and hypotheses about the first, third, and fourth vertical arrows. The conclusion is something about the second vertical arrow.
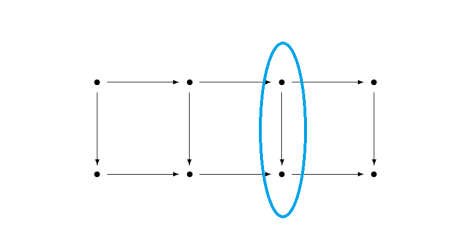
The second part of the lemma is very similar, but has hypotheses about the first, second, and fourth vertical arrows and concludes something about the third arrow.
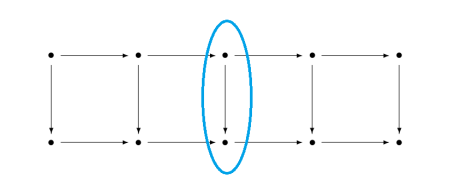
The five lemma starts with a commutative diagram with five objects across the top and bottom rows.
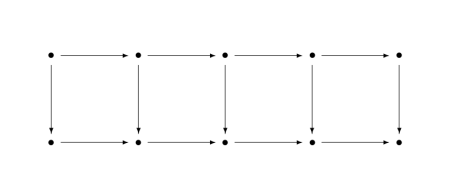
Given assumptions about every arrow except the vertical arrow in the middle, the theorem concludes something about the middle arrow.
The nine lemma, a.k.a. the 3*3 lemma, starts with a commutative diagram of the following shape.
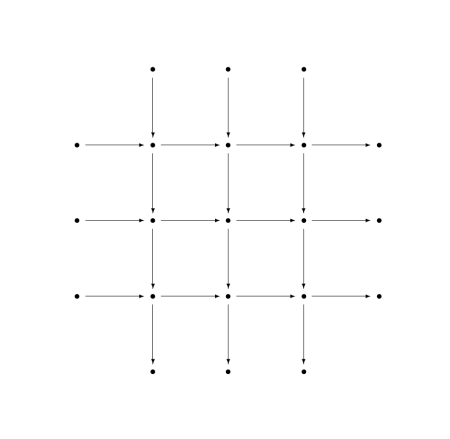
It's called the nine lemma because the attention is focused on the nine dots, the 3*3 grid of dots in the middle. All the objects around the perimeter, those outside the 3*3 grid, are 0.
There are three parts to the nine lemma. Each has hypotheses about all the columns and two of the rows, and concludes something about the row that was left out. So, for example, one part of the theorem has hypotheses about the three columns and the first two rows and concludes something about the last row.
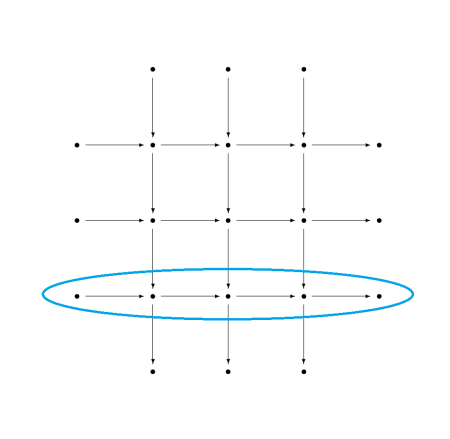
Here I zoom in from 100,000 feet to 10,000 feet, giving some of the missing details but not all. For full details, you could look up the theorems on Wikipedia or on nLab.
As promised at the beginning, this was a ridiculously high-level view of these theorems. The purpose was to point out the core of each theorem and making it possible to compare the three theorems at the highest level.
When I said a theorem makes a hypothesis about a row or a column, the hypothesis is that the row forms an exact sequence. The conclusions in the nine lemma are that a row is an exact sequence.
When I alluded to hypotheses about vertical arrows, these hypotheses are essentially saying that a function is one-to-one (injective), onto (surjective), or one-to-one and onto (bijective). More precisely, they are assumptions that a morphism is mono, epi, or iso. More on this terminology here. The conclusion of the four lemma is that an arrow is either epi or mono. The conclusion of the five lemma is that an arrow is iso.
Related postsThe post Four, five, and nine lemmas first appeared on John D. Cook.