Linear logic arithmetic
Linear logic has connectives not used in classical logic. The connectives and & are conjunctions, and are disjunctions, and ! and ? are analogous to the modal operators  and (necessity and possibility).
and (necessity and possibility).
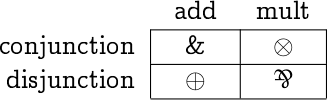
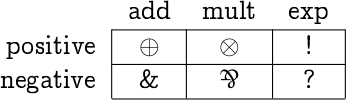
Another way to classify the connectives is to say and & are called additive, and are multiplicative, and ! and ? are called exponential.And still another classification says that , , and ! have positive polarity, while &, , and ? have negative polarity.
This post will show that these arithmetical names are justified by analogy.
For one thing, multiplication-like connectives distribute over addition-like connectives.
2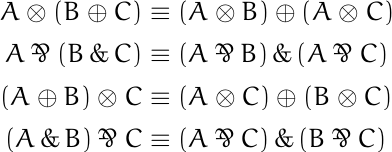
Also, the exponential-like operators behave analogously to the equation
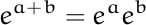
with respect to the addition-like and multiplication-like connectives.
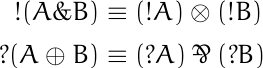
In both equations, if you apply an exponential-like operator to the result of applying an addition-like operator, you get a multiplication-like operator applied to the exponential-like operator applied to two addition-like arguments separately.
The term polarity" is justified by the fact that linear negation flips the polarity of connectives.
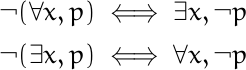
In the following analogs of De Morgan's laws, negation turns conjunctions into disjunctions and vice versa, and it reverses the polarity of connectives.
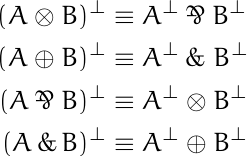
Negating exponential connectives also flips polarity.
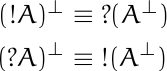
These rules are analogous to the rules for negating quantifiers in classical logic.