Zip codes, geocodes, and Hilbert curves
You might think that if zip codes are close, then the regions they represent are close. Or that if zip codes are consecutive, then their regions touch. Neither of these are true. I explore how far they are from being true in the next post.
But these statements could have been true [1]. It's possible to lay a grid on a region and number the squares in the grid in such a way that consecutive numbers correspond to contiguous squares, and nearby numbers correspond to nearby squares. There are geocoding systems that accomplish this using Hilbert curves. For example, Google's S2 system is based on Hilbert curves.
A Hilbert curve is a curve that winds through a square, coming arbitrarily close to every point in the square. A Hilbert curve is a fractal, defined as the limit of an iterative process. We aren't concerned with the limit because we only want to carry out a finite number of steps in the construction. But the fact that the limit exists tells us that with enough steps we can get any resolution we want.
To illustrate Hilbert curves and how they could be used to label grids, we will use a Hilbert curve to tour a chessboard. We will number the squares of a chess board so that consecutive numbers correspond to neighboring squares.
Here's Python code to produce our numbering.
from hilbertcurve.hilbertcurve import HilbertCurve p = 3 # 2^3 squares on a side n = 2 # two dimensional cube, i.e. square hc = HilbertCurve(p, n) for row in range(2**p): for col in range(2**p): d = hc.distance_from_point([row, col]) print(format(d,"2d"), " ", end="") print()
This produces the following output.
0 1 14 15 16 19 20 21 3 2 13 12 17 18 23 22 4 7 8 11 30 29 24 25 5 6 9 10 31 28 27 26 58 57 54 53 32 35 36 37 59 56 55 52 33 34 39 38 60 61 50 51 46 45 40 41 63 62 49 48 47 44 43 42
Here's Python code to draw lines rather than print numbers.
N = (2**p)**n points = hc.points_from_distances(range(N)) for i in range(1, N): x0, y0 = points[i-1] x1, y1 = points[i] plt.plot([x0, x1], [y0, y1]) plt.gca().set_aspect('equal') plt.show()This produces the following image.
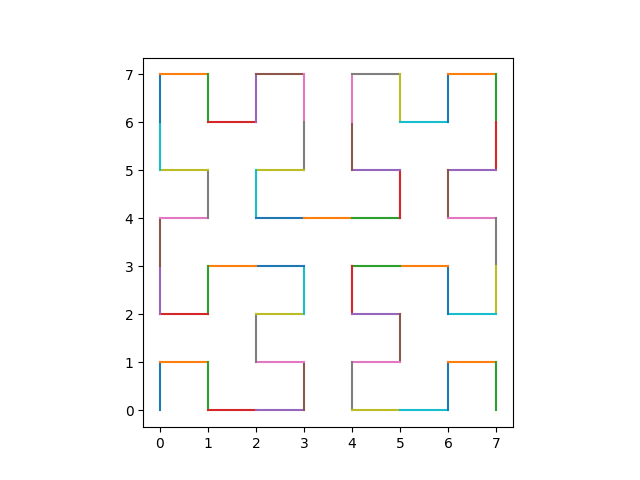
There's a small problem. Following the square numberings above produces a Hilbert curve, and the plotting code produces and Hilbert curve, but they're not the same Hilbert curve. The implicit axes created by our sequence of print statements doesn't match the geometry in the plotting code. To get the curves to match we need to do a sort of change of coordinates. We can do this by changing the call to plt.plot to
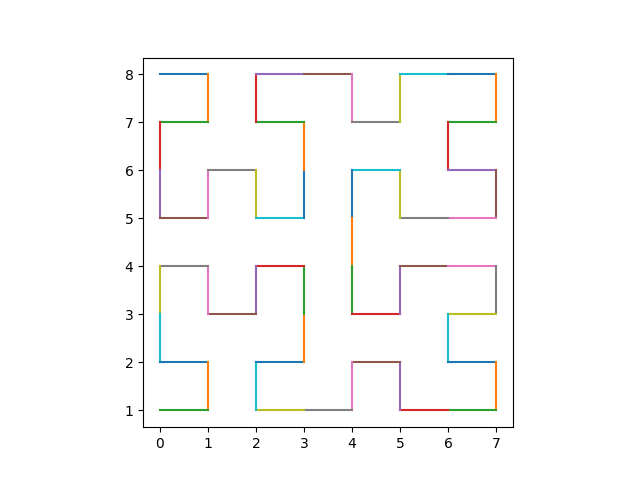
plt.plot([y0, y1], [8-x0, 8-x1])
This produces the following plot, matching the numbering above.
[1] It could have been true in the sense that it was theoretically possible. It might not have been practically possible. Postal codes have different design constraints than geocodes.
The post Zip codes, geocodes, and Hilbert curves first appeared on John D. Cook.