Numerically evaluating a theta function
Theta functions pop up throughout pure and applied mathematics. For example, they're common in analytic number theory, and they're solutions to the heat equation.
Theta functions are analogous in some ways to trigonometric functions, and like trigonometric functions they satisfy a lot of identities. This post will comment briefly on an identity that makes a particular theta function, 3, easy to compute numerically. And because there are identities relating the various theta functions, a method for computing 3 can be used to compute other theta functions.
The function 3 is defined by
where
Here's a plot of 3 with t = 1 + i
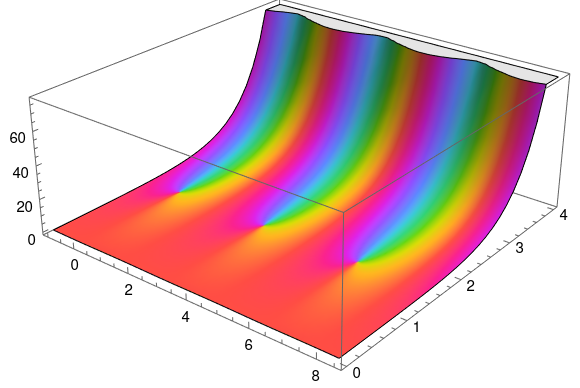
produced by the following Mathematica code:
q = Exp[Pi I (1 + I)] ComplexPlot3D[EllipticTheta[3, z, q], {z, -1, 8.5 + 4 I}]An important theorem tells us
This theorem has a lot of interesting consequences, but for our purposes note that the identity has the form
The important thing for numerical purposes is that t is on one side and 1/t is on the other.
Suppose t = a + bi with a > 0 and b > 0. Then
Now if b is small, |q| is near 1, and the series defining 3 converges slowly. But if b is large, |q| is very small, and the series converges rapidly.
So if b is large, use the left side of the theorem above to compute the right. But if b is small, use the right side to compute the left.
Related postsThe post Numerically evaluating a theta function first appeared on John D. Cook.