Bump functions
A bump function is a smooth (i.e. infinitely differentiable) function that is positive on some open interval (a, b) and zero outside that interval. I mentioned bump functions a few weeks ago and discussed how they could be used to prevent clicks in radio transmissions.
Today I ran into a twitter thread that gave a more general construction of bump functions that I'd seen before. The thread concludes with this:
You can create bump functions by this recipe:
- Take any f(x) growing faster than polynomial (e.g. exp)
- Define g(x) = 1 / f(1/x)
- Let h(x) = g(1+x) g(1-x).
- Zero out x(-1,1)
- Scale, shift, etc
In this post I'll give a quick asymptotic proof that the construction above works.
Let a positive integer n be given and define g(x) to be zero for negative x. We'll show that if f grows faster than xn. then g is n times differentiable at 0.
As x , f(x) is eventually bounded below by a function growing faster than xn. And so as x 0, f(1/x) grows faster than xn and 1/f(1/x) goes to zero faster than xn, and so its nth derivative is zero.
It follows that g(1 + x) is n times differentiable at -1 and g(1 - x) is n times differentiable at 1. So h is n times differentiable at -1 and 1. The function h is positive on the open interval (-1, 1) and zero outside. Our choice of n was arbitrary, so h is infinitely differentiable, and so h is a bump function. We could shift and scale h to make it a bump function on any other finite interval.
DiscussionWhen I was a student, I would have called this kind of proof hand waving. I'd want to see every inequality made explicit: there exists some M > 0 such that for x > M .... Now I find arguments like the one above easier to follow and more convincing. I imagine if a lecturer gives a proof with all the inequalities spelled out, he or she is probably thinking about something like the proof above and expanding the asymptotic argument on the fly.
Note that a slightly more general theorem falls out of the proof. Our goal was to show if f grows faster than every polynomial, then g and h are infinitely differentiable. But along the way we proved, for example, that if f eventually grows like x7 then g and h are six-times differentiable.
In fact, let's look at the case f(x) = x7.
f[x_] := x^7 g[x_] := If[x > 0, 1/ f[1/x], 0] h[x_] := g[x + 1] g[1 - x] Plot[h[x], {x, -1.5, 1.5}]This produces the following plot.
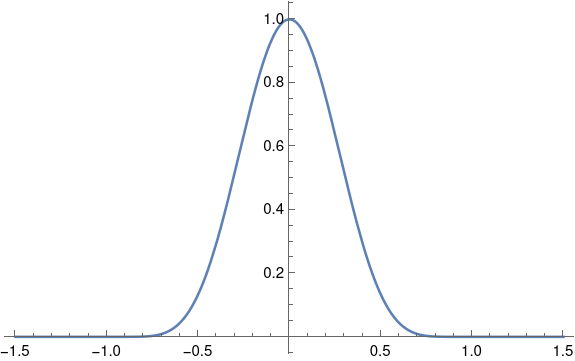
Just looking at the plot, h looks smooth; it's plausible that it has six derivatives. It appears h is zero outside [-1, 1] and h is positive over at least part of [-1, 1]. If you look at the Mathematica code you can convince yourself that h really is positive on the entire interval open interval (-1, 1), though it is very small as it approaches either end.
Related postsThe post Bump functions first appeared on John D. Cook.