Circles and lines under a Möbius transformation

This post will revisit a previous post in more detail. I've written before about how Mobius transformations map circles and lines to circles and lines. In this post I'd like to explore how you'd calculate which circle or line a given circle or line goes to. Given an equation of a line or circle, what is the equation of its image?

Circles to circles

A while back I wrote a post called Circles to Circles, demonstrating how Mobius transformations map circles and lines to circles and lines. If you think of a line as a degenerate circle, a circle of infinite radius, then you could simply say Mobius transformations map circles to circles.

For example I showed in that post that the transformation

m(z) = (z + 2)/(3z + 4)

maps these circles

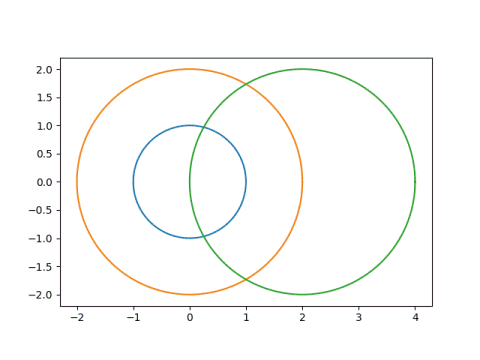
to these circles

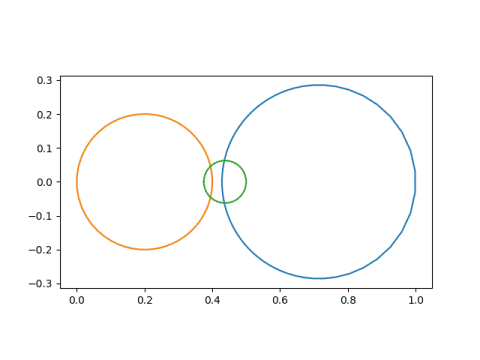
and that these lines

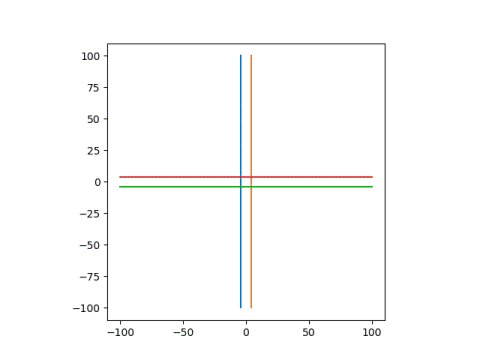
go to these circles

Circle or line image

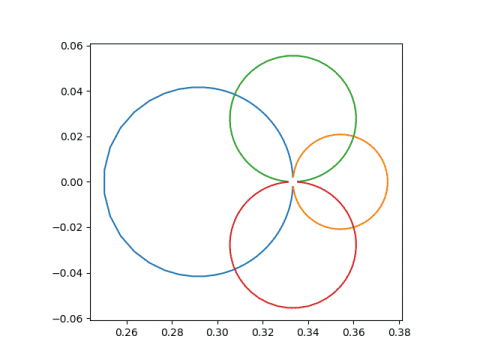
Given the equation of a circle or a line, how would you know whether its image is a circle or a line?

A Mobius transformation

m(z) = (az + b) / (cz + d)

has a singularity at z = -d/c. If a line or curve goes through the point -d/c then its image is a line. Otherwise the image is a circle.

If the line or curve does go through -d/c, so that the image is a line, it's easy to find an equation of the line. Pick two points, z₁ and z₂ on the original curve or line. Let w₁ - m(z₁) and w₂ - m(z₂). Then find the equation of a line through w₁ and w₂. For example, a parametric form is

w₁ + t(w₂ - w₁)

for all real t.

Equation of the image circle

Now suppose we start with a circle centered at with radius r. We apply

m(z) = (az + b) / (cz + d)

as above, but we assume our circle does not pass through -d/c since that case is covered above. With this assumption we can conclude that the image of our circle is another circle, and the remaining task is to find an equation of that circle.

We can decompose our transformation m into several simpler steps-translation, reciprocal, rotation, and dilation-and see what happens to the center and radius under each step. The hardest step is taking the reciprocal, and this is covered in the previous post. That post was a lemma for this post.

We can apply m to z in four steps:

1. Add d/c.
2. Take the reciprocal.
3. Multiply by e = (bc - ad)/c^2.
4. Add a/c.

We know it's OK to take the reciprocal in the second step because our circle does not contain the point z = -d/c.

We can break step 3 into (3a) multiplying by |e| and (3b) multiplying by e/|e|. Step 3a is a dilation and step 3b is a rotation.

Here's a Python program using the steps above to find the center and radius of a transformed circle.

 def transform(a, b, c, d, center, radius): # step 1 center += d/c # step 2 temp = center center = np.conj(center) / (abs(center)**2 - radius**2) radius /= abs(abs(temp)**2 - radius**2) # step 3 e = (b*c - a*d)/c**2 center *= e radius *= abs(e) # step 4 center += a/c return (center, radius)

The post Circles and lines under a Mobius transformation first appeared on John D. Cook.