Adding a tiny trap to stop chaos
The tent map is a famous example of a chaotic function. We will show how a tiny modification of the tent maps retains continuity of the function but prevents chaos.
The tent map is the function f: [0, 1] [0, 1] defined by
This map has an unstable fixed point at x0 = 2/3. If you start exactly at x0, then you'll stay there forever as you keep iteratively applying f. But if you start a tiny bit away from x0, you'll move away from your starting point and bounce around throughout the interval [0, 1].
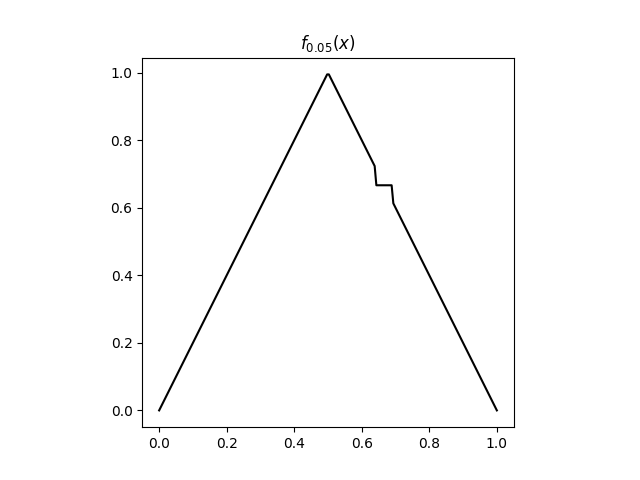
Now pick some positive less than 1/6 [1] and modify the function f on the interval
I =[x0 - , x0 + ]
as described in [2]. To do this, we define f to be the same as f outside the interval I. We then create a flat spot in the middle of the interval by defining f to be x0 on
[x0 - /2, x0 + /2]
and extend f linearly on the rest of I.
Here's a plot of f with = 0.05.
Now here's a cobweb plot of the iterates of f0.05 starting at - 3.
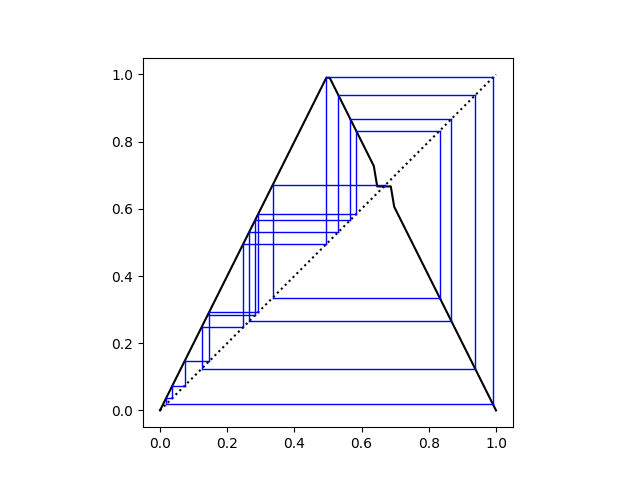
The iterates of f always converge to x0 in finite time. If the iterates ever wander into the interval [x0 - /2, x0 + /2] then they get trapped at x0. And because the tent map is ergodic, nearly all sequences will wander into the entrapping interval.
Here's Python code to make the construction of f explicit.
def tent(x): if x x0 + epsilon: return tent(x) x1 = x0 - epsilon/2 x2 = x0 + epsilon/2 if x > x1 and x Revenge of floating point
In theory, almost all starting points should lead to sequences that converge to x0 in finite time. But it took a fair amount of trial and error to come up the plot above that illustrates this. For most starting points that I tried, the sequence of iterates converged to 0.
Now 0 is an unstable fixed point. This is easy to see: if x ever gets close to 0, the next iterate is 2x, twice as far from 0. Iterates keep getting doubled until they're larger than 1/2. How can this be?
Computers can only represent fractions with some power of 2 in the denominator. And I believe the tent map (not the modified tent map with a trap) will always converge to 0 when starting with a floating point number.
Here are the iterates of the tent map starting at (the floating point representation of) - 3:
0 0.28318530717958623
1 0.5663706143591725
2 0.8672587712816551
3 0.26548245743668986
...
29 0.13050460815429688
30 0.26100921630859375
31 0.5220184326171875
32 0.955963134765625
33 0.08807373046875
34 0.1761474609375
35 0.352294921875
36 0.70458984375
37 0.5908203125
38 0.818359375
39 0.36328125
40 0.7265625
41 0.546875
42 0.90625
43 0.1875
44 0.375
45 0.75
46 0.5
47 1.0
48 0.0
Note that the sequence doesn't sneak up on 0: it leaps from 1 to 0. So this does not contract the argument above that points near zero are repelled away.
[1] Why less than 1/6? So we stay in the same branch of the definition of f. The distance from x0 to 1/2 is 1/6.
[2] Achim Clausing, Ducci Matrices. American Mathematical Monthly, December 2018.
The post Adding a tiny trap to stop chaos first appeared on John D. Cook.